题目内容
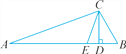
【题目】如图,已知AB∥CD,AC∥BD,CE平分∠ACD.
(1)求证:△ACE是等腰三角形;
(2)求证:∠BEC>∠BDC.
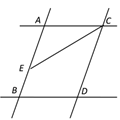
【答案】(1)证明见解析;(2)证明见解析
【解析】分析:(1)根据AB∥CD,得∠AEC=∠ECD,再根据角平分线的定义得出∠ACE=∠ECD,从而得出∠AEC=∠ECA,根据等角对等边,得出AC=AE;
(2)先判断ABDC为平行四边形,根据平行四边形的性质得出∠CAE=∠BDC,再根据外角的性质得出∠BEC>∠BDC.
本题解析:
(1)∵AB∥CD,
∴∠AEC=∠ECD,
∵CE平分∠ACD,
∴∠ACE=∠ECD,
∴∠AEC=∠ECA,
∴AC=AE,
∴△ACE是等腰三角形;
(2)∵AB∥CD,AC∥BD,
∴四边形ABDC为平行四边形,
∴∠CAE=∠BDC,
∵∠BEC>∠CAE,
∴∠BEC>∠BDC.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目