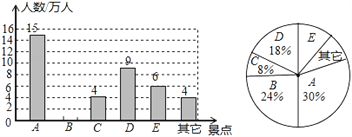
题目内容
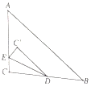
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是BC边的中点,E是AC边上的任意一点,△DCE和△DC′E关于直线DE对称,若点C′ 恰好落在△ABC的中位线上,则CE的长度为_______.
【答案】![]() 或
或![]() .
.
【解析】
分别画了三角形的三条中位线,根据题意C′只能落在DF和FG上,分别画出图形,设CE=x,利用勾股定理列方程求出x的值即可.
解:取AC,AB的中点F,G,连结DF,FG,GD.
① 如图,当点C′落在DF上时,
∵D为BC的中点,
∴DC′=DC=![]() BC=4,
BC=4,
在Rt△ABC中,AC=6,BC=8,
∴AB=![]() =10,
=10,
∵D,F分别为中点,
∴DF=![]() AB=5,
AB=5,
∴FC′= DF- DC′=5-4=1,
设CE=CE′=x,则EF=3-x,
在Rt△EFC′中,
![]() ,
,
∴![]() ,
,
解得,x=![]() ,
,
∴CE=![]() .
.
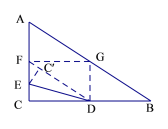
② 如图,当点C′落在FG上时,
∵D,G分别为各边中点,
∴DG=3,
又DC′=DC=4,
在Rt△DGC′中,
![]() =
=![]() ,
,
∵F,G分别为各边中点,
∴FG=![]() BC=4,
BC=4,
∴FC′=FG-GC′=4-![]() ,
,
设EC=EC′=x,则EF=3-x,
在Rt△EFC′中,
![]() ,
,
∴![]() ,
,
解得,x=![]() ,
,
∴CE=![]() .
.

综上,CE的值为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目