题目内容
 已知:如图所示的长方形ABCD沿EF折叠至D1、C1位置,若∠C1FE=115°,求∠AED1度数.
已知:如图所示的长方形ABCD沿EF折叠至D1、C1位置,若∠C1FE=115°,求∠AED1度数.分析:根据折叠可得:∠C1FE=∠EFC,再根据平行线的性质可得∠EFC+∠FEB=180°,进而得到∠FEB,再计算出∠AED1度数即可.
解答:解:∵∠C1FE=115°,
∴∠EFC=115°,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠EFC+∠FEB=180°,
∴∠FEB=180°-115°=65°,
根据折叠可得∠BEF=∠FED1=65°,
∴∠AED1=180°-65°-65°=50°.
∴∠EFC=115°,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠EFC+∠FEB=180°,
∴∠FEB=180°-115°=65°,
根据折叠可得∠BEF=∠FED1=65°,
∴∠AED1=180°-65°-65°=50°.
点评:此题主要考查了平行线的性质以及图形的折叠,关键是掌握图形折叠后哪些角是对应相等的.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
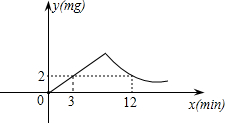 得点燃药物后3min与12min,室内每立方米空气中的含药量为2mg.据以上信息解答下列问题:
得点燃药物后3min与12min,室内每立方米空气中的含药量为2mg.据以上信息解答下列问题: 为预防“甲流H1N1病毒”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
为预防“甲流H1N1病毒”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题: 为预防“甲型H1N1”流感,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
为预防“甲型H1N1”流感,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题: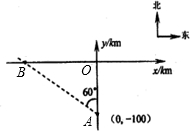 侵袭,那么台风从生成到最初侵袭C城要经过多长时间?(本问中
侵袭,那么台风从生成到最初侵袭C城要经过多长时间?(本问中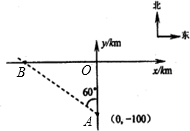 侵袭,那么台风从生成到最初侵袭C城要经过多长时间?(本问中
侵袭,那么台风从生成到最初侵袭C城要经过多长时间?(本问中 取1.7)
取1.7)