题目内容
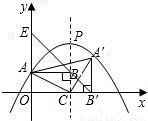
(2007•莆田)如图,抛物线y=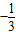 x2+
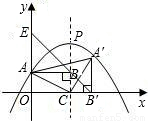
x2+ mx+n(其中m,n为常数且m>n)与y轴正半轴交于A点,它的对称轴交x轴正半轴于C点,抛物线的顶点为P,Rt△ABC的直角顶点B在对称轴上,当它绕点C按顺时针方向旋转90°得到Rt△A′B′C.
mx+n(其中m,n为常数且m>n)与y轴正半轴交于A点,它的对称轴交x轴正半轴于C点,抛物线的顶点为P,Rt△ABC的直角顶点B在对称轴上,当它绕点C按顺时针方向旋转90°得到Rt△A′B′C.(1)写出点A,P,A′的坐标(用含m,n的式子表示);
(2)若直线BB'交y轴于E点,求证:线段B′E与AA′互相平分;
(3)若点A′在抛物线上且Rt△ABC的面积为1时,请求出抛物线的解析式并判断在抛物线的对称轴上是否存在点D,使△AA′D为等腰三角形?若存在,请直接写出所有符合条件的D点坐标;若不存在,请说明理由.
【答案】分析:(1)根据抛物线的解析式易得出A点和P点的坐标.根据旋转的性质可看得出AB=A′B′,BC=B′C,因此A′的横坐标为P点的横坐标与A点横坐标的和,而A′的纵坐标与P点的横坐标相等,由此可得出A′的坐标.
(2)在直角三角形BCB′中,BC=B′C,因此三角形BCB′是等腰直角三角形,即∠EBA=∠BB′C=45°,可得出EA=AB=A′B′,这样就证得了四边形AEA′B′是平行四边形,那么根据平行四边形的性质即可得出所证的条件.
(3)①根据A′在抛物线上,将A′的坐标代入抛物线的解析式中可得出一个关于m,n的等量关系.已知了三角形ABC的面积为1,可得出另一个关于m、n的等量关系,联立两式即可求出m、n的值,也就求出了A、A′的坐标.
②本题可分三种情况:
一:AD=A′D;二:AD=AA′;三:AA′=A′D;
可根据对称轴方程设出D点坐标,然后根据坐标系中两点间的距离公式来列等量关系进而可求出D的坐标.
解答:(1)解:令x=0,得到y=n,
∴A(0,n),且m>n>0
∵y=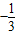 x2+
x2+ mx+n=
mx+n=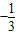 (x-m)2+
(x-m)2+ m2+n,
m2+n,
∴P(m, m2+n).
m2+n).
根据题意得,∠ABC=∠AOC=∠OCB=90°,
∴四边形ABCO是矩形.
∴BC=AO=B′C=n,AB=A′B′=OC=m.
∴A′点坐标为(m+n,m).
(2)证明:连接EA′,AB′.
∵BC=B′C,∠BCB′=90°,
∴∠EB′O=45°.
∵∠EOB′=90°,
∴∠OEB′=45°,
∴OB′=OE=m+n.
∵AO=n,
∴EA=m,∵A′B′=m,
∴A′B′=EA(5分)
∵∠A′B′C=90°,
∴EA∥A′B′.
∴四边形AEA′B′是平行四边形.
∴对角线B′E与AA′互相平分.
(3)解:∵点A′(m+n,m)在抛物线上,
∴m=- (m+n)2+
(m+n)2+ (m+n)m+n.
(m+n)m+n.
整理得:m-n= (m+n)(m-n)
(m+n)(m-n)
∵m>n,即m-n≠0.
∴m+n=3,即n=3-m.
∵ AB•BC=1,即
AB•BC=1,即 mn=1.
mn=1.
把n=3-m代入 m•n=1
m•n=1
得, m(3-m)=1.
m(3-m)=1.
解得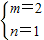 或
或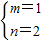 (不合题意舍去)
(不合题意舍去)
∴抛物线解析式为y=- x2+
x2+ x+1.
x+1.
∴A'(3,2),A(0,1).
结论:在抛物线的对称轴上存在点D,使△AA′D为等腰三角形.
点D的坐标为:D1(2,1+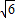 ),D2(2,1-
),D2(2,1- ),D3(2,5),D4(2,-1),D5(2,0).
),D3(2,5),D4(2,-1),D5(2,0).
点评:本题为二次函数综合题,考查了图形的旋转变换、平行四边形的判定和性质、等腰三角形的判定等知识点,综合性强,能力要求较高.考查学生分类讨论,数形结合的数学思想方法.
(2)在直角三角形BCB′中,BC=B′C,因此三角形BCB′是等腰直角三角形,即∠EBA=∠BB′C=45°,可得出EA=AB=A′B′,这样就证得了四边形AEA′B′是平行四边形,那么根据平行四边形的性质即可得出所证的条件.
(3)①根据A′在抛物线上,将A′的坐标代入抛物线的解析式中可得出一个关于m,n的等量关系.已知了三角形ABC的面积为1,可得出另一个关于m、n的等量关系,联立两式即可求出m、n的值,也就求出了A、A′的坐标.
②本题可分三种情况:
一:AD=A′D;二:AD=AA′;三:AA′=A′D;
可根据对称轴方程设出D点坐标,然后根据坐标系中两点间的距离公式来列等量关系进而可求出D的坐标.
解答:(1)解:令x=0,得到y=n,
∴A(0,n),且m>n>0
∵y=
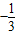 x2+
x2+ mx+n=
mx+n=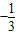 (x-m)2+
(x-m)2+ m2+n,
m2+n,∴P(m,
 m2+n).
m2+n).根据题意得,∠ABC=∠AOC=∠OCB=90°,
∴四边形ABCO是矩形.
∴BC=AO=B′C=n,AB=A′B′=OC=m.
∴A′点坐标为(m+n,m).
(2)证明:连接EA′,AB′.
∵BC=B′C,∠BCB′=90°,
∴∠EB′O=45°.
∵∠EOB′=90°,
∴∠OEB′=45°,
∴OB′=OE=m+n.
∵AO=n,
∴EA=m,∵A′B′=m,
∴A′B′=EA(5分)
∵∠A′B′C=90°,
∴EA∥A′B′.
∴四边形AEA′B′是平行四边形.
∴对角线B′E与AA′互相平分.
(3)解:∵点A′(m+n,m)在抛物线上,
∴m=-
 (m+n)2+
(m+n)2+ (m+n)m+n.
(m+n)m+n.整理得:m-n=
 (m+n)(m-n)
(m+n)(m-n)∵m>n,即m-n≠0.
∴m+n=3,即n=3-m.
∵
 AB•BC=1,即
AB•BC=1,即 mn=1.
mn=1.把n=3-m代入
 m•n=1
m•n=1得,
 m(3-m)=1.
m(3-m)=1.解得
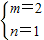 或
或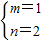 (不合题意舍去)
(不合题意舍去)∴抛物线解析式为y=-
 x2+
x2+ x+1.
x+1.∴A'(3,2),A(0,1).
结论:在抛物线的对称轴上存在点D,使△AA′D为等腰三角形.
点D的坐标为:D1(2,1+
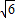 ),D2(2,1-
),D2(2,1- ),D3(2,5),D4(2,-1),D5(2,0).
),D3(2,5),D4(2,-1),D5(2,0).点评:本题为二次函数综合题,考查了图形的旋转变换、平行四边形的判定和性质、等腰三角形的判定等知识点,综合性强,能力要求较高.考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目
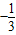 x2+
x2+ mx+n(其中m,n为常数且m>n)与y轴正半轴交于A点,它的对称轴交x轴正半轴于C点,抛物线的顶点为P,Rt△ABC的直角顶点B在对称轴上,当它绕点C按顺时针方向旋转90°得到Rt△A′B′C.
mx+n(其中m,n为常数且m>n)与y轴正半轴交于A点,它的对称轴交x轴正半轴于C点,抛物线的顶点为P,Rt△ABC的直角顶点B在对称轴上,当它绕点C按顺时针方向旋转90°得到Rt△A′B′C.