ĢāÄæÄŚČŻ
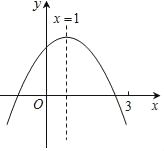
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬”÷ABCµÄ¶„µć ![]() ŌŚ
ŌŚ ![]() Öįøŗ°ėÖįÉĻ£¬¶„µć
Öįøŗ°ėÖįÉĻ£¬¶„µć![]() ŌŚ
ŌŚ![]() ÖįÕż°ėÖįÉĻ£¬¶„µć
ÖįÕż°ėÖįÉĻ£¬¶„µć ![]() ŌŚµŚŅ»ĻóĻŽ£¬Ļ߶Ī
ŌŚµŚŅ»ĻóĻŽ£¬Ļ߶Ī ![]() £¬
£¬![]() µÄ³¤ŹĒŅ»ŌŖ¶ž“Ī·½³Ģ
µÄ³¤ŹĒŅ»ŌŖ¶ž“Ī·½³Ģ ![]() µÄĮ½øł£¬
µÄĮ½øł£¬![]() £¬
£¬![]() £®
£®
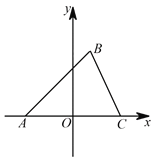
£Ø1£©Ö±½ÓŠ“³öµć![]() µÄ×ų±ź µć C µÄ×ų±ź £»
µÄ×ų±ź µć C µÄ×ų±ź £»
£Ø2£©Čō·“±ČĄżŗÆŹż![]() µÄĶ¼Ļó¾¹żµć
µÄĶ¼Ļó¾¹żµć![]() £¬Ēó
£¬Ēó ![]() µÄÖµ£»
掙术
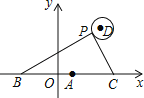
£Ø3£©ČēĶ¼¹żµć![]() ×÷
×÷![]() ÖįÓŚµć
ÖįÓŚµć ![]() £»ŌŚ
£»ŌŚ![]() ÖįÉĻŹĒ·ń“ęŌŚµć
ÖįÉĻŹĒ·ń“ęŌŚµć ![]() £¬Ź¹ŅŌ
£¬Ź¹ŅŌ![]() £¬
£¬![]() £¬
£¬![]() ĪŖ¶„µćµÄČż½ĒŠĪÓėŅŌ
ĪŖ¶„µćµÄČż½ĒŠĪÓėŅŌ![]() £¬
£¬![]() £¬
£¬![]() ĪŖ¶„µćµÄČż½ĒŠĪĻąĖĘ?Čō“ęŌŚ£¬Ö±½ÓŠ“³öĀś×ćĢõ¼žµÄµć
ĪŖ¶„µćµÄČż½ĒŠĪĻąĖĘ?Čō“ęŌŚ£¬Ö±½ÓŠ“³öĀś×ćĢõ¼žµÄµć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©![]() £¬
£¬![]() £®£Ø2£©
£®£Ø2£©![]() £»£Ø3£©“ęŌŚ£¬
£»£Ø3£©“ęŌŚ£¬![]() »ņ
»ņ ![]() »ņ
»ņ ![]() »ņ
»ņ ![]() »ņ
»ņ ![]()
”¾½āĪö”æ
£Ø1£©½āŅ»ŌŖ¶ž“Ī·½³Ģx2-12x+36=0£¬Ēó³öĮ½øł¼“æɵƵ½µćA£¬CµÄ×ų±ź£»
£Ø2£©¹żµćB×÷BE”ĶAC£¬“¹×ćĪŖE£¬ÓÉ”ĻBAC=45”ćæÉÖŖAE=BE£¬ÉčBE=x£¬ÓĆ¹“¹É¶ØĄķæɵĆCE=![]() £¬øł¾ŻAE+CE=OA+OC£¬½ā·½³ĢĒó³öBE£¬ŌŁÓÉAE-OA=OE£¬¼“æÉĒó³öµćBµÄ×ų±ź£¬Č»ŗóĒó³ökµÄÖµ£»
£¬øł¾ŻAE+CE=OA+OC£¬½ā·½³ĢĒó³öBE£¬ŌŁÓÉAE-OA=OE£¬¼“æÉĒó³öµćBµÄ×ų±ź£¬Č»ŗóĒó³ökµÄÖµ£»
£Ø3£©·ÖĄąĢÖĀŪ£¬øł¾ŻĻąĖĘČż½ĒŠĪ¶ŌÓ¦±ß³É±ČĄżĒó³öµćPµÄ×ų±ź£®
£Ø1£©½āŅ»ŌŖ¶ž“Ī·½³Ģ ![]() £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
ĖłŅŌ ![]() £¬
£¬
ĖłŅŌ ![]() £¬
£¬![]() £»
£»
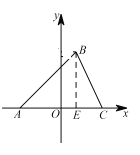
£Ø2£© ČēĶ¼£¬¹żµć ![]() ×÷
×÷ ![]() £¬“¹×ćĪŖ
£¬“¹×ćĪŖ ![]() £¬
£¬
”ß ![]() £¬
£¬
”ą ![]() £¬
£¬
Éč![]() £¬
£¬
”ß ![]() =12£¬
=12£¬
”ą EC=12-x£¬
ŌŚRt¦¤BECÖŠ£¬![]() £¬
£¬
”ą ![]()
ÕūĄķµĆ£ŗ![]() £¬
£¬
½āµĆ£ŗ![]() £Ø²»ŗĻĢāŅāÉįČ„£©£¬
£Ø²»ŗĻĢāŅāÉįČ„£©£¬![]() £¬
£¬
”ą ![]() £¬
£¬![]() £¬
£¬
”ą ![]() £¬
£¬

°Ń![]() “śČė
“śČė![]() £¬µĆ
£¬µĆ ![]() £»
£»
£Ø3£©“ęŌŚ£®
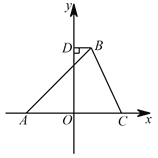
ČēĶ¼2£¬
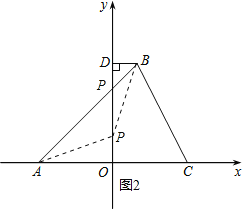
ČōµćPŌŚODÉĻ£¬Čō”÷PDB”×”÷AOP£¬
Ōņ![]() £¬¼“
£¬¼“![]() £¬
£¬
½āµĆ£ŗOP=2»ņOP=6£¬
”ąP£Ø0£¬2£©»ņP£Ø0£¬6£©£»
ČēĶ¼3£¬

ČōµćPŌŚODÉĻ·½£¬”÷PDB”×”÷AOP£¬
Ōņ![]() £¬¼“
£¬¼“![]() £¬
£¬
½āµĆ£ŗOP=12£¬
”ąP£Ø0£¬12£©£»
ČēĶ¼4£¬
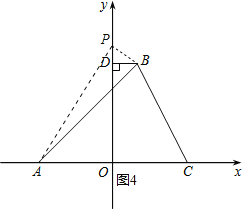
ČōµćPŌŚODÉĻ·½£¬”÷BDP”×”÷AOP£¬
Ōņ![]() £¬¼“
£¬¼“![]() £¬
£¬
½āµĆ£ŗOP=4+2![]() »ņOP=4-2
»ņOP=4-2![]() £Ø²»ŗĻĢāŅāÉįČ„£©£¬
£Ø²»ŗĻĢāŅāÉįČ„£©£¬
”ąP£Ø0£¬4+2![]() £©£»
£©£»
ČēĶ¼5£¬
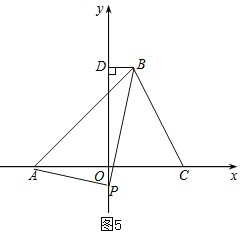
ČōµćPŌŚyÖįøŗ°ėÖį£¬”÷PDB”×”÷AOP£¬
Ōņ![]() £¬¼“
£¬¼“![]() £¬
£¬
½āµĆ£ŗOP=-4+2![]() »ņ-4-2
»ņ-4-2![]() £Ø²»ŗĻĢāŅāÉįČ„£©£¬
£Ø²»ŗĻĢāŅāÉįČ„£©£¬
ŌņPµć×ų±źĪŖ£Ø0£¬4-2![]() £©
£©
¹Źµć ![]() µÄ×ų±źĪŖ£ŗ
µÄ×ų±źĪŖ£ŗ![]() »ņ
»ņ ![]() »ņ
»ņ ![]() »ņ
»ņ ![]() »ņ
»ņ ![]()