题目内容
【题目】我们给出如下新定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
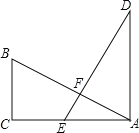
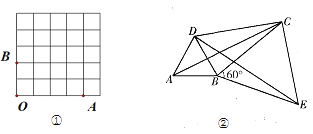
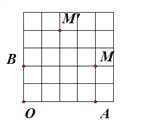
(1)如图①,请你在图中画出格点M,使得四边形OAMB是以OA、OB为勾股边且对角线相等的勾股四边形;
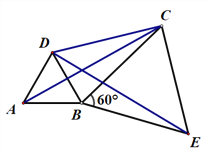
(2)如图②,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC,CE.若∠DCB=30°,则四边形ABCD是勾股四边形,为什么?
【答案】(1)图形见解析(2)证明见解析
【解析】试题分析:(1)根据题意,利用勾股定理计算画出即可;(2)根据旋转的性质证出△BCE为等边三角形;再利用等边三角形的性质,得出△DCE是直角三角形,问题得解.
试题解析:
(1)
(2)证:由旋转可知:BC=BE,∠CBE=60°,
∵∠CBF=60°,
∴△BCE是等边三角形,
∴EC=BC,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
∴DC2+EC2=DE ,
∴DC2+BC2=AC ,
∴四边形ABCD是勾股四边形.

练习册系列答案
相关题目
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率