题目内容
已知A、B表示两个不同的多项式,且A-B=x3-1,A=-2x3+2x-3,求多项式B.
分析:根据A-B=x3-1,A=-2x3+2x-3,直接求出多项式B即可.
解答:解:∵A-B=x3-1,A=-2x3+2x-3,
∴B=A-(x3-1)
=-2x3+2x-3-(x3-1)
=-3x3+2x-2.
∴B=A-(x3-1)
=-2x3+2x-3-(x3-1)
=-3x3+2x-2.
点评:本题考查了整式的加减,解答本题的关键实际上就是去括号、合并同类项,这是各地中考的常考点.

练习册系列答案
相关题目
已知a,b表示两个非零的有理数,则
+
的值不可能是( )
| |a| |
| a |
| |b| |
| b |
| A、2 | B、-2 | C、1 | D、0 |
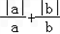 的值不可能是
的值不可能是