题目内容
已知二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1、x2,且x1<x2,则下列结论中:①方程kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2;②当x=-2时,y=1;③当x>x2时,y>0;④x1<-1,x2>-1.其中正确的结论是
- A.①②
- B.①②③
- C.①②④
- D.①③④
C
分析:把相应的x的值代入;二次函数与x轴的交点即为转换为一元二次方程等于0的解;与-1相关就加上1后应用相关不等式整理结果;两根相减需确定二次项系数的符号.
解答:②把x=-2直接代入函数式可得y=1,正确;
③因不知道k的符号,就不知道开口方向,无法确定,错误;
①因为二次函数数y=kx2+(2k-1)x-1与x轴有两个交点,所以,方程kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2,正确;
④∵(x1+1)(x2+1)=x1x2+x1+x2+1=-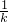 -
-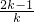 +1=-1<0,又x1<x2,
+1=-1<0,又x1<x2,
∴x1+1<x2+1,x1+1<0,x2+1>0,即x1<-1,x2>-1,正确.
∴正确的结论是①②④.
故选C.
点评:主要考查了二次函数的性质与一元二次方程的根,及根与系数之间的关系.
分析:把相应的x的值代入;二次函数与x轴的交点即为转换为一元二次方程等于0的解;与-1相关就加上1后应用相关不等式整理结果;两根相减需确定二次项系数的符号.
解答:②把x=-2直接代入函数式可得y=1,正确;
③因不知道k的符号,就不知道开口方向,无法确定,错误;
①因为二次函数数y=kx2+(2k-1)x-1与x轴有两个交点,所以,方程kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2,正确;
④∵(x1+1)(x2+1)=x1x2+x1+x2+1=-
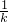 -
-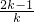 +1=-1<0,又x1<x2,
+1=-1<0,又x1<x2,∴x1+1<x2+1,x1+1<0,x2+1>0,即x1<-1,x2>-1,正确.
∴正确的结论是①②④.
故选C.
点评:主要考查了二次函数的性质与一元二次方程的根,及根与系数之间的关系.

练习册系列答案
相关题目
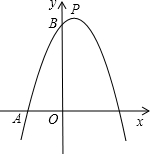 点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过点A、点B.
点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过点A、点B. 已知二次函数y=ax2+bx+3图象的对称轴为直线x=1.
已知二次函数y=ax2+bx+3图象的对称轴为直线x=1.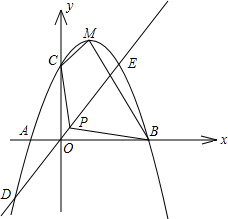 为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.