题目内容

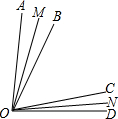如图，OM平分∠AOB、ON平分∠COD，若∠AOD=84°，∠MON=68°，求∠BOC．
分析：根据角平分线定义可得∠AOM=∠BOM=x，∠CON=∠DON=y，再根据图形可得∠BOC=68°-（x+y），∠AOD=2x+68°-（x+y）+2y=84°，化简可得x+y=16°，进而得到∠BOC的度数．
解答：解：设∠AOM=∠BOM=x，∠CON=∠DON=y，则∠BOC=68°-（x+y）．
∴2x+68°-（x+y）+2y=84°，
x+y=16°，
∴∠BOC=68°-16°=52°．
点评：此题主要考查了角的计算，关键是理清图中角的相等关系，与和差关系．
练习册系列答案
相关题目
25、如图1，在平面直角坐标系xoy中，直线y=x+6与x轴交于A，与y轴交于B，BC⊥AB交x轴于C．
①求△ABC的面积．
②如图2，D为OA延长线上一动点，以BD为直角边做等腰直角三角形BDE，连接EA．求直线EA的解析式．
③点E是y轴正半轴上一点，且∠OAE=30°，OF平分∠OAE，点M是射线AF上一动点，点N是线段AO上一动点，是判断是否存在这样的点M、N，使得OM+NM的值最小，若存在，请写出其最小值，并加以说明．
（2013•徐州模拟）已知：在如图1所示的平面直角坐标系xOy中，A、C两点的坐标分别为A（4，2），C（n，-2）（其中n＞0），点B在x轴的正半轴上．动点P从点O出发，在四边形OABC的边上依次沿O-A-B-C的顺序向点C移动，当点P与点C重合时停止运动．设点P移动的路径的长为l，△POC的面积为S，S与l的函数关系的图象如图2所示，其中四边形ODEF是等腰梯形．
（1）结合以上信息及图2填空：图2中的m=
2
5
2
5
；
（2）求B、C两点的坐标及图2中OF的长；
（3）若OM是∠AOB的角平分线，且点G与点H分别是线段AO与射线OM上的两个动点，直接写出HG+AH的最小值，请在图3中画出示意图并简述理由．
（2012•沈阳）已知，如图①，∠MON=60°，点A，B为射线OM，ON上的动点（点A，B不与点O重合），且AB=4
3
，在∠MON的内部，△AOB的外部有一点P，且AP=BP，∠APB=120°．
（1）求AP的长；
（2）求证：点P在∠MON的平分线上．
（3）如图②，点C，D，E，F分别是四边形AOBP的边AO，OB，BP，PA的中点，连接CD，DE，EF，FC，OP．
①当AB⊥OP时，请直接写出四边形CDEF的周长的值；
②若四边形CDEF的周长用t表示，请直接写出t的取值范围．
如图1，已知A （0，a），B（b，0），点P为△ABO的角平分线的交点．

（1）若a、b满足|a+b|+a2-4a+4=0．求A、B的坐标；
（2）连OP，在（1）的条件下，求证：OP+OB=AB；
（3）如图2．PM⊥PA交x轴于M，PN⊥AB于N，试探究：AO-OM与PN之间的数量关系．

已知，如图①，∠MON=60°，点A、B为射线OM、ON上的动点（点A、B不与点O重合），且AB=，在∠MON的内部、△AOB的外部有一点P，且AP=BP，∠APB=120°.

 

（1）求AP的长；

（2）求证：点P在∠MON的平分线上；

（3）如图②，点C，D，E，F分别是四边形AOBP的边AO，OB，BP，PA的中点，连接CD，DE，EF，FC，OP.

①当AB⊥OP时，请直接写出四边形CDEF的周长；

②若四边形CDEF的周长用t表示，请直接写出t的取值范围．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网