题目内容
 22、如图所示,在三角形纸片ABC中,∠C=90°,∠B=30°,按如下步骤可以把这个直角三角形纸片分成三个全等的小直角三角形(图中虚线表示折痕):①先将点B对折到点A,②将对折后的纸片再沿AD对折.
22、如图所示,在三角形纸片ABC中,∠C=90°,∠B=30°,按如下步骤可以把这个直角三角形纸片分成三个全等的小直角三角形(图中虚线表示折痕):①先将点B对折到点A,②将对折后的纸片再沿AD对折.(1)由步骤①可以得到哪些等量关系?
(2)请证明△ACD≌△AED;
(3)按照这种方法能否将任意一个直角三角形分成三个全等的小三角形.
分析:(1)此题要理解折叠的实质是重合,根据重合可以得到AE=BE,AD=BD,∠B=∠DAE=30°,∠BDE=∠ADE=60°,∠AED=∠BED=90°;
(2)根据(1)结合直角三角形中30°所对的直角边等于斜边的一半这个结论可以得到△ACD和△AED全等的条件,然后再证明;
(3)不能把任意一个直角三角形分成三个全等的小三角形,因为根据全等容易求出直角三角形三个角的度数,是30°,60°,90°,所以不能达到要求.
(2)根据(1)结合直角三角形中30°所对的直角边等于斜边的一半这个结论可以得到△ACD和△AED全等的条件,然后再证明;
(3)不能把任意一个直角三角形分成三个全等的小三角形,因为根据全等容易求出直角三角形三个角的度数,是30°,60°,90°,所以不能达到要求.
解答:解:(1)AE=BE,AD=BD,∠B=∠DAE=30°,
∠BDE=∠ADE=60°,∠AED=∠BED=90°.
(2)在Rt△ABC中,∠B=30°,所以AE=EB,因而AC=AE
又因为∠CAD=∠EAD,AD=AD所以△ACD≌△AED;
(3)不能.
∠BDE=∠ADE=60°,∠AED=∠BED=90°.
(2)在Rt△ABC中,∠B=30°,所以AE=EB,因而AC=AE
又因为∠CAD=∠EAD,AD=AD所以△ACD≌△AED;
(3)不能.
点评:此题是折叠问题,是学生的难点,要求学生理解折叠的实质是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图所示,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是:
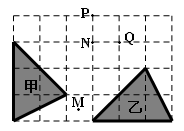

| A.点M | B.格点N | C.格点P | D.格点Q |
如图所示,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是:


| A.点M | B.格点N | C.格点P | D.格点Q |


