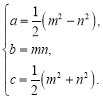题目内容
【题目】如图,已知y=3x+3与x轴交于点B,与y轴交于点A,与函数y=x的图象交于点P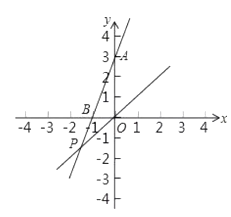
(1)在该坐标系中画出函数y= ![]()
![]() 的图象,并说明点P也在函数y=
的图象,并说明点P也在函数y= ![]()
![]() 的图象上;
的图象上;
(2)设直线y= ![]() 与x轴交于点C,与y轴交于点D,求证:PO平分∠APC;
与x轴交于点C,与y轴交于点D,求证:PO平分∠APC;
(3)连接AC,求△APC的面积;
(4)在y轴上,是否存在点M,使△ACM为等腰三角形?若存在,请直接写出符合条件的所有点M的坐标;若不存在,请说明理由。
【答案】
(1)解:如图,解方程组,得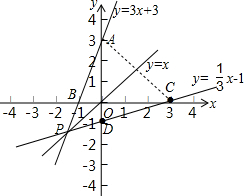
|
得
|
,
则P点坐标为(-
3 |
2 |
,-
3 |
2 |
),
当x=-
3 |
2 |
时,y=
1 |
3 |
x(![]() -1=
-1=
1 |
3 |
×(-
3 |
2 |
)-1=-
3 |
2 |
,所以点P在函数y=![]() x-1
x-1
的图象上 |
(2)证明:∵点A(0,3)和点C(3,0)关于直线y=x对称,
∴直线y=x垂直平分AC,
∴PO平分∠APC;
(3)解:B(-1,0),A(0,3),
△APC的面积=S△ABC+S△PBC
= ![]() ×(3+1)×3+
×(3+1)×3+ ![]() ×(3+1)×3=9.
×(3+1)×3=9.
(4)AC=![]() ,
,
当AC=AM时,OM=AM-OA=![]() -3,M坐标为(0,3-
-3,M坐标为(0,3-![]() )或(0,3+
)或(0,3+![]() );
);
当CA=CM时,OA=OM=3,M坐标为(0.-3);
当MA=MC时,M在原点,坐标为(0,0)
【解析】
(1)两直线相交或平行:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同,由此可进行求解.(2)可证明PO所在三角形为等腰三角形,即直线y=x垂直平分AC,可得到平分顶角;(4)等腰三角形需分为三类,A、C、M分别为顶角顶点,由等腰三角形的性质可求出M坐标.

练习册系列答案
相关题目