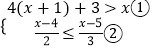Question

【题目】解方程组或不等式组
（1）
；
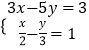
（2）
；
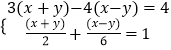
（3）
；
（4）
．

Answer 1

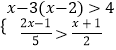
【答案】
（1）解：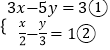

由②，可得：3x﹣2y=6③，

③﹣①，可得：3y=3，

解得y=1，

把y=1代入①，解得x= ，

∴原方程组的解是

（2）解：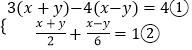

由①，可得：x=7y﹣4③，

把③代入②，解得y= ，

∴x=7× ﹣4= ，

∴原方程组的解是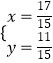

（3）解：

解不等式①，得x＞﹣2，

解不等式②，得x≤2，

∴这个不等式组的解集是﹣2＜x≤2

（4）解：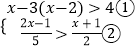

解不等式①，得x＜1，

解不等式②，得x＜﹣7，

∴这个不等式组的解集是x＜﹣7

【解析】本题主要考查用消元法解二元一次方程组.利用加减消元法消去x，解得y值，代入原方程组，解得x值，可得到原方程组的解.

【考点精析】解答此题的关键在于理解解二元一次方程组的相关知识，掌握二元一次方程组：①代入消元法；②加减消元法，以及对一元一次不等式组的解法的理解，了解解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )．