��Ŀ����
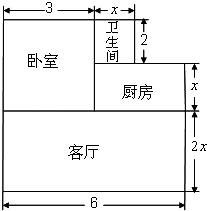
����Ŀ����֪��CΪ�߶�AB��һ�㣬�ֱ���AC��BCΪ�����߶�ABͬ������ACD�͡�BCE����CA=CD��CB=CE����ACD=��BCE��ֱ��AE��BD���ڵ�F
��1����ͼ1������ACD=60�b�����AFB= ��
��2����ͼ2������ACD=�������AFB= ���ú�����ʽ�ӱ�ʾ����
��3����ͼ2�еġ�ACD�Ƶ�C˳ʱ����ת����Ƕȣ�����F������BD��AE�е�һ���߶��ϣ�����ͼ3����̽����AFB�����������ϵ��������֤����
���𰸡�(1)120��;(2) 180��D��;(3)������
�������������������1�������ACE=��DCB��֤��ACE�ա�DCB���Ƴ���CAE=��CDB�������AFB=��CDA+��DAC�������������ڽǺͶ���������ɣ�
��2�������ACE=��DCB��֤��ACE�ա�DCB���Ƴ���CAE=��CDB�������AFB=��CDA+��DAC�������������ڽǺͶ������������
��3�������ACE=��DCB��֤��ACE�ա�DCB���Ƴ���CAE=��CDB�������AFB=��CEB+��CBE�������������ڽǺͶ������������
����������⣺��1���ߡ�ACD=��BCE�����ACD+��DCE=��BCE+��DCE�����ACE=��DCB������ACE����DCB��

����ACE����DCB�����CAE=��CDB�����AFB=��CDB+��CDA+��DAE
=��CDA+��DAE+��BAE
=��CDA+��DAC
=180��D60��
=120����
��2���⣺�ߡ�ACD=��BCE�����ACD+��DCE=��BCE+��DCE�����ACE=��DCB������ACE����DCB��
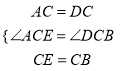
����ACE����DCB�����CAE=��CDB�����AFB=��CDB+��CDA+��DAE
=��CDA+��DAE+��BAE
=��CDA+��DAC
=180��D��ACD
=180��D����
��3����AFB=180-����֤�����ߡ�ACD=��BCE�����ACD+��DCE=��BCE+��DCE�����ACE=��DCB������ACE����DCB��
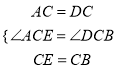
����ACE����DCB�����AEC=��DBC�����AFB=��AEC+��CEB+��EBD
=��DBC+��CEB+��EBC
=��CEB+��EBC
=180��-��ECB
=180��-����