题目内容
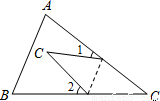
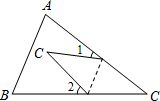如图，纸片△ABC中，∠A=55°，∠B=75°，将纸片的一角折叠，使C落在△ABC内，则∠1+∠2等于（ ）分析：根据三角形内角和定理可得∠3+∠4=∠A+∠B，再根据折叠的性质可得∠5+∠6=∠3+∠4，然后根据平角等于180°列式计算即可得解．
解答：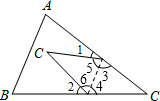
解：根据三角形内角和定理，∠3+∠4=180°-∠C，
∠A+∠B=180°-∠C，
所以，∠3+∠4=∠A+∠B，
根据折叠的性质，∠5+∠6=∠3+∠4，
∵∠1+∠5+∠3+∠2+∠6+∠4=2×180°，
∴∠1+∠2+2（∠A+∠B）=360°，
∵∠A=55°，∠B=75°，
∴∠1+∠2+2（55°+75°）=360°，
解得∠1+∠2=100°．
故选C．
解：根据三角形内角和定理，∠3+∠4=180°-∠C，∠A+∠B=180°-∠C，
所以，∠3+∠4=∠A+∠B，
根据折叠的性质，∠5+∠6=∠3+∠4，
∵∠1+∠5+∠3+∠2+∠6+∠4=2×180°，
∴∠1+∠2+2（∠A+∠B）=360°，
∵∠A=55°，∠B=75°，
∴∠1+∠2+2（55°+75°）=360°，
解得∠1+∠2=100°．
故选C．
点评：本题考查了三角形的内角和定理，翻折的性质，求出∠1+∠2与∠A、∠B的关系是解题的关键，要注意整体思想的利用．
练习册系列答案
相关题目
如图三角形纸片ABC中，∠A=75°，∠B=60°，将纸片的角折叠，使点C落在△ABC内，若∠α=35°，则∠β=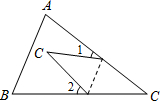
如图，纸片△ABC中，∠A=55°，∠B=75°，将纸片的一角折叠，使C落在△ABC内，则∠1+∠2等于
如图三角形纸片ABC中，∠A=75°，∠B=60°，将纸片的角折叠，使点C落在△ABC内，若∠α=35°，则∠β=________．