题目内容
如图三角形纸片ABC中，∠A=75°，∠B=60°，将纸片的角折叠，使点C落在△ABC内，若∠α=35°，则∠β=________．
55°
分析：首先根据四边形内角和定理可得：∠α+∠β+（180°-∠C）+∠A+∠B=360°，再算出∠C的度数，代入相应数值，即可算出∠β．
解答：根据四边形内角和定理可得：∠α+∠β+（180°-∠C）+∠A+∠B=360°，
∵∠A=75°，∠B=60°，
∴∠C=45°，
∵∠α=35°，
∴35°+∠β+180°-45°+75°+60°=360°，
解得∠β=55°．
故答案为：55°．
点评：本题主要考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
分析：首先根据四边形内角和定理可得：∠α+∠β+（180°-∠C）+∠A+∠B=360°，再算出∠C的度数，代入相应数值，即可算出∠β．
解答：根据四边形内角和定理可得：∠α+∠β+（180°-∠C）+∠A+∠B=360°，
∵∠A=75°，∠B=60°，
∴∠C=45°，
∵∠α=35°，
∴35°+∠β+180°-45°+75°+60°=360°，
解得∠β=55°．
故答案为：55°．
点评：本题主要考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
练习册系列答案
星级口算天天练系列答案
相关题目
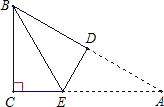在三角形纸片ABC中，∠C=90°，∠A=30°，AC=3，折叠该纸片，使点A与点B重合，折痕与AB、AC分别相交于点D和点E（如图），折痕DE的长为
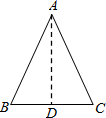如图，已知ABC为等腰三角形纸片ABC底边，将此三角形纸片对折，使腰AB、AC重合，折痕为AD，则折痕AD与底边BC的关系是
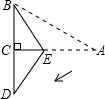如图所示，已知在三角形纸片ABC中，BC=3，AB=6，∠BCA=90°，在AC上取一点E，以BE为折痕翻折△ABC，使AB的一部分与BC重合，A与BC延长线上的点D重合，则线段AD的长度为（ ）
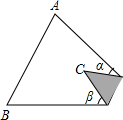如图三角形纸片ABC中，∠A=75°，∠B=60°，将纸片的角折叠，使点C落在△ABC内，若∠α=35°，则∠β=