题目内容
【题目】如图,在△ABC中,D为AB的中点,DE∥BC,交AC于点E,DE∥AC,交BC于点F.
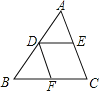
(1)求证:DE=BF;
(2)连接EF,请你猜想线段EF和AB有何关系?并对你的猜想加以证明.
【答案】(1)见解析;(2)EF∥AB且 EF=![]() AB,见解析
AB,见解析
【解析】
试题分析:(1)利用平行线的性质得到相等的角,证明△ADE≌△DBF,即可得到DE=BF.
(2)EF∥AB且 EF=![]() AB,证明△DBF≌△FED,得到EF=BD=
AB,证明△DBF≌△FED,得到EF=BD=![]() AB,∠BDF=∠DFE,所以EF∥AB.
AB,∠BDF=∠DFE,所以EF∥AB.
(1)∵D为AB的中点,
∴AD=DB,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C
∵DF∥AC,
∴∠DFB=∠C,
∴∠AED=∠DFB,
在△ADE和△DBF中,
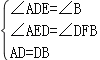
∴△ADE≌△DBF,
∴DE=BF.
(2)EF∥AB且 EF=![]() AB,如图,
AB,如图,
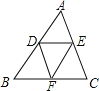
∵DE∥BC,
∴∠EDF=∠DFB,
在△DBF和△FED中,
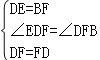
∴△DBF≌△FED
∴EF=BD=![]() AB,∠BDF=∠DFE,
AB,∠BDF=∠DFE,
∴EF∥AB.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目