题目内容
已知a、b满足3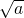 +5|b|=7(a≥0),则s=2
+5|b|=7(a≥0),则s=2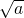 -3|b|的取值范围为
-3|b|的取值范围为
- A.-
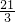 <s<
<s<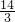
- B.-
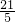 ≤s≤
≤s≤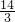
- C.-
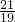 ≤s≤
≤s≤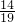
- D.以上都不对
B
分析:可以由已知条件:用a表示b或用b表示a.再根据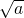 和|b|都是非负数,即可求得S的最大值和最小值.
和|b|都是非负数,即可求得S的最大值和最小值.
解答:∵a,b满足 ,
,
∴|b|=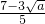 =
=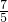 -
- ;
;
又∵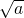 和|b|都是非负数,
和|b|都是非负数,
∴0≤2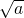 ≤
≤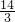 ,
,
同理-3|b|≥-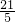
∴S最大值=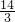 ;
;
S最小值=0-3×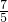 =-
=-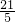 ;
;
∴-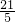 ≤S≤
≤S≤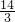 .
.
故选B.
点评:本题考查了函数的最值问题.注意能用一个字母表示另一个字母,从而用一个字母表示S,再结合二次根式的性质进行分S析,即可得出S的最大值和最小值.
分析:可以由已知条件:用a表示b或用b表示a.再根据
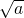 和|b|都是非负数,即可求得S的最大值和最小值.
和|b|都是非负数,即可求得S的最大值和最小值.解答:∵a,b满足
 ,
,∴|b|=
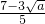 =
=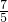 -
- ;
;又∵
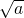 和|b|都是非负数,
和|b|都是非负数,∴0≤2
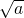 ≤
≤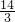 ,
,同理-3|b|≥-
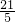
∴S最大值=
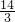 ;
;S最小值=0-3×
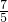 =-
=-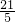 ;
;∴-
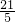 ≤S≤
≤S≤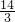 .
.故选B.
点评:本题考查了函数的最值问题.注意能用一个字母表示另一个字母,从而用一个字母表示S,再结合二次根式的性质进行分S析,即可得出S的最大值和最小值.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目