题目内容
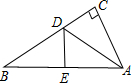 如图,有一个直角三角形ABC,两直角边AC=6cm,BC=8cm,AD平分∠BAC,点E在斜边AB上且AE=AC.
如图,有一个直角三角形ABC,两直角边AC=6cm,BC=8cm,AD平分∠BAC,点E在斜边AB上且AE=AC.(1)△BED是何特殊三角形?说明理由;(2)求线段CD的长.
分析:(1)根据AE=AC,可判定△ACD≌△AED,由∠C=90°,得∠AED=90°,从而判断出△BED是直角三角形;
(2)△BDE∽△BAC,利用相似比求得线段CD的长.
(2)△BDE∽△BAC,利用相似比求得线段CD的长.
解答:解:(1)△BED是直角三角形,理由是:
∵AD平分∠BAC,∴∠CAD=∠EAD,∵AE=AC,AD为公共边,∴△ACD≌△AED,∴∠AED=∠C=90°,∴∠BED=90°,
∴△BED是直角三角形;
(2)∵△ACD≌△AED,∴DC=DE,∠B+∠BDE=90°,
∵∠B+∠BAC=90°,∴∠BDE=∠BAC,∴△BDE∽△BAC,∴
=
,
∵两直角边AC=6cm,BC=8cm,∴AB=10cm,
∴
=
,解得CD=3.
∵AD平分∠BAC,∴∠CAD=∠EAD,∵AE=AC,AD为公共边,∴△ACD≌△AED,∴∠AED=∠C=90°,∴∠BED=90°,
∴△BED是直角三角形;
(2)∵△ACD≌△AED,∴DC=DE,∠B+∠BDE=90°,
∵∠B+∠BAC=90°,∴∠BDE=∠BAC,∴△BDE∽△BAC,∴
| DE |
| AC |
| BD |
| AB |
∵两直角边AC=6cm,BC=8cm,∴AB=10cm,
∴
| CD |
| 6 |
| 8-CD |
| 10 |
点评:本题考查了证明两个三角形全等和相似,以及勾股定理的应用.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 互唯一确定的.
互唯一确定的. .
. .
.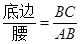 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.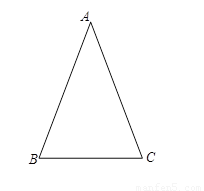
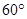 的值为( ▼ )
的值为( ▼ )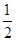 B.
1 C.
B.
1 C. 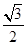 D.
2
D.
2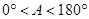 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .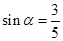 ,其中
,其中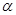 为锐角,试求sad
为锐角,试求sad .
. .
. .
. .
.