Question

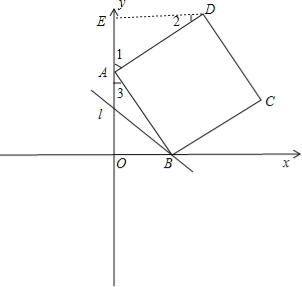
【题目】在平面直角坐标系xOy中，点A（0，4），B（3，0），以AB为边在第一象限内作正方形ABCD，直线L：y=kx+3．

（1）当直线l经过D点时，求点D的坐标及k的值；

（2）当直线L与正方形有两个交点时，直接写出k的取值范围．

Answer 1

【答案】（1）D（4，7），k=1；（2）k＞﹣1

【解析】试题分析：（1）过D点作DE⊥y轴，证△AED≌△BOA，根据全等求出DE=AO=4，AE=OB=3，即可得出D的坐标，把D的坐标代入解析式即可求出k的值；

（2）把B的坐标代入求出K的值，即可得出答案．

试题解析：解：（1）如图，过D点作DE⊥y轴，

则∠AED=∠1+∠2=90°．

在正方形ABCD中，∠DAB=90°，AD=AB．

∴∠1+∠3=90°，

∴∠2=∠3．

又∵∠AOB=∠AED=90°，

在△AED和△BOA中，

，

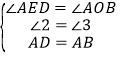∴△AED≌△BOA，

∴DE=AO=4，AE=OB=3，

∴OE=7，

∴D点坐标为（4，7），

把D（4，7）代入y=kx+3，得k=1；

（2）当直线y=kx+3过B点时，把（3，0）代入得：0=3k+3，

解得：k=﹣1．

所以当直线l与正方形有两个交点时，k的取值范围是k＞﹣1．