题目内容
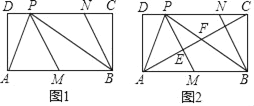
【题目】如图,正方形ABCD,将边CD绕点C顺时针旋转60°,得到线段CE,连接DE,AE,BD交于点F.
(1)求∠AFB的度数;
(2)求证:BF=EF;
(3)连接CF,直接用等式表示线段AB,CF,EF的数量关系.

【答案】(1)∠AFB=60°;(2)见解析;(3)![]() AB+CF=2EF.
AB+CF=2EF.
【解析】
(1)根据正方形的性质得∠ADB=45°,再有旋转图形的边相等,则对应的底角也相等求出∠DAE=∠DEA=15°,从而得到∠AFB=60°.
(2)由等边三角形及∠DEA=15°,得到∠CEF=∠CBF=45°,再结合已知根据SAS证明△ADF≌△CDF,再由角的代换证明出△ECF≌△BCF,从而证明BF=EF.
(3过C作CG⊥BD于G,由已知求出∠GCF=30°从而得到CF=2FG,设FG=x,从而求出![]() AB+CF=2
AB+CF=2![]() x+2x,EF=BF=BG+FG=x+
x+2x,EF=BF=BG+FG=x+![]() x,最终得到
x,最终得到![]() AB+CF=2EF.
AB+CF=2EF.
解:(1)∵四边形ABCD是正方形,
∴∠ADB=![]() ∠ADC=45°,
∠ADC=45°,
由旋转得:CD=CE,∠DCE=60°,
∴△DCE是等边三角形,
∴CD=DE=AD,∠ADE=90°+60°=150°,
∴∠DAE=∠DEA=15°,
∴∠AFB=∠FAD+∠ADB=15°+45°=60°;
(2)连接CF,

∵△CDE是等边三角形,
∴∠DEC=60°,
∵∠DEA=15°,
∴∠CEF=∠CBF=45°,
∵四边形ABCD是正方形,
∴AD=CD,∠ADF=∠CDF=45°,
∵DF=DF,
∴△ADF≌△CDF(SAS),
∴∠DAF=∠DCF=15°,
∴∠FCB=90°﹣15°=75°,∠ECF=60°+15°=75°,
∴∠FCB=∠ECF,
∵CF=CF,
∴△ECF≌△BCF(SAS),
∴BF=EF;
(3)![]() AB+CF=2EF,理由是:
AB+CF=2EF,理由是:
过C作CG⊥BD于G,

∵∠CBD=45°,
∴△CGB是等腰直角三角形,
∵∠BCF=75°,
∴∠GCF=30°,
∴CF=2FG,
设FG=x,则CF=2x,CG=BG=![]() x,
x,
∴BC=AB=![]() CG=
CG=![]() x,
x,
∴![]() AB+CF=2
AB+CF=2![]() x+2x,EF=BF=BG+FG=x+
x+2x,EF=BF=BG+FG=x+![]() x,
x,
∴![]() AB+CF=2EF.
AB+CF=2EF.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案