题目内容
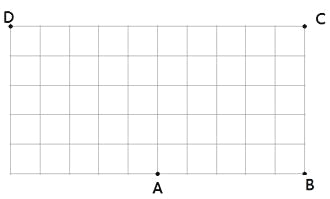
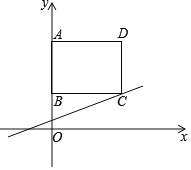
【题目】如图，在平面直角坐标系中，矩形ABCD的顶点A、B、D的坐标分别为（0，5）、（0，2）、（4，5），直线l的解析式为y＝kx+2﹣4k（k＞0）．
（1）当直线l经过原点O时，求一次函数的解析式；
（2）通过计算说明：不论k为何值，直线l总经过点C；
（3）在（1）的条件下，点M为直线l上的点，平面内是否存在x轴上方的点N，使以点O、A、M、N为顶点的四边形是菱形？若存在，请直接写出点M的坐标：若不存在，请说明理由．
【答案】（1）
；（2）详见解析；（3）存在，满足条件的点M为
或
或
．
【解析】
（1）将原点坐标代入解析式可求出k的值，即可求解；
（2）由题意可得点C（4，2），当x＝4时，y＝4k+2﹣4k＝2，则可得不论k为何值，直线l总经过点C；
（3）分OA为边，OA为对角线两种情况讨论，由菱形的性质可求解．
解：（1）∵直线l经过原点，
∴把点（0，0）代入y＝kx+2﹣4k，
得：2﹣4k＝0，
解得：
，
∴一次函数的解析式为：；
（2）由题意可知，点C的坐标为（4，2），
当x＝4时，y＝4k+2﹣4k＝2，
∴不论k为何值，直线l总经过点C；
（3）设点M（x，
x）
①以OA为菱形的边，此时，OM＝OA＝5，
∴
∴x＝±2
，
点M的坐标为或；
②以OA为菱形的一条对角线，
此时MN垂直平分OA，
则x＝
∴x＝5
则M的坐标为；
综上所述：满足条件的点M为或或．
【题目】某校数学兴趣小组，对函数y＝|x﹣1|+1的图象和性质进行了探究，探究过程如下：
（1）自变量x的取值范围是全体实数，x与y的几组对应值如表：
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | … |
其中m＝ ．
（2）如图，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象：
（3）根据画出的函数图象特征，仿照示例，完成下列表格中的函数变化规律：
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在直线x＝1的右侧，函数图象呈上升状态 | 当x＞1时，y随x的增大而增大 |
① | 在直线x＝1的左侧，函数图象呈下降状态 |
|
示例2 | 函数图象经过点（﹣3，5） | 当x＝﹣3时，y＝5 |
② | 函数图象的最低点是（1，1） |
|
（4）当2＜y≤4时，x的取值范围为 ．
