Question

（本小题满分8分）

　已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE = AF．

（1）求证：BE = DF；

（2）连接AC交EF于点O，延长OC至点M，使OM = OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．

 

Answer 1

【答案】

 

（1）BE = DF，证明略。

（2）四边形AEMF是菱形，证明略。

【解析】

证明：（1）∵四边形ABCD是正方形，

∴AB＝AD,∠B = ∠D = 90°．

∵AE = AF，

∴．

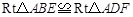∴BE＝DF．                   4分

（2）四边形AEMF是菱形．

∵四边形ABCD是正方形，

∴∠BCA = ∠DCA = 45°，BC = DC．

∵BE＝DF，

∴BC－BE = DC－DF. 即．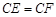

∴．

∵OM = OA，

∴四边形AEMF是平行四边形．

∵AE = AF，

∴平行四边形AEMF是菱形．       8分