Question

【题目】如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE.将△ADE 沿AE对折至△AFE，延长EF交边BC于点G，连接AG，CF.

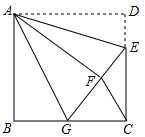
求证：(1)△ABG≌△AFG;

(2)求△FGC的面积．

Answer 1

【答案】（1）证明见解析；（2）3.6.

【解析】

试题分析：（1）利用翻折变换对应边关系得出AB=AF，∠B=∠AFG=90°，利用HL定理得出△ABG≌△AFG即可；

（2）利用勾股定理得出GE2=CG2+CE2，进而求出BG即可；

（3）首先过C作CM⊥GF于M，由勾股定理以及由面积法得，CM=2.4，进而得出答案．

试题解析：（1）在正方形ABCD中，AD=AB=BC=CD，∠D=∠B=∠BCD=90°，

∵将△ADE沿AE对折至△AFE，

∴AD=AF，DE=EF，∠D=∠AFE=90°，

∴AB=AF，∠B=∠AFG=90°，

又∵AG=AG，

在Rt△ABG和Rt△AFG中，

∵

∴△ABG≌△AFG（HL）；

（2）过C作CM⊥GF于M，

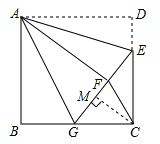
∵BG=GF=3，

∴CG=3，EC=6-2=4，

∴GE==5，

CMGE=GCEC，

∴CM×5=3×4，

∴CM=2.4，

∴S△FGC=GF×CM=3.6．