Question

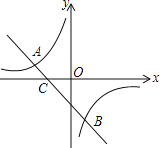
【题目】如图，在平面直角坐标系中（请补画出必要的图形），为坐标原点，直线y=-2x+4与、轴分别交于、两点，过线段的中点作轴的垂线，分别与直线交于点，与直线y=x+n交于点.

（1）直接写出点A、B、C、的坐标：A（____________），B（____________），C（_____________），D（____________）；

（2）若的面积等于1，求点P的坐标.

Answer 1

【答案】(1)（ 2，0 ）,（0，4）,（1，0）,（ 1，2 ）;(2)点P的坐标为：P或 .

【解析】分析: （1）将x=0，y=0代入y=-2x+4可求出点A和点B的坐标，根据点C是AB的中点求出点C的坐标，最后根据CD∥y轴，即可求出点D的坐标.

(2)根据的面积等于1,可得=1,即可求出的值,根据绝对值的定义求出n的值.

详解:

（1）A（ 2，0 ），（0，4），C（1，0），D（ 1，2 ），

（2） ∵点是直线与直线的交点，

直线⊥轴，且过点，

∴（1， ）

∴

∴

∴

解得: = －1或=3

∴点P的坐标为：P或

点睛: 此题主要考查了一次函数图象上点的坐标性质以及两直线相交问题等知识，得出A，B，C，D点坐标是解题关键．