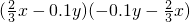题目内容
下列各式中，不能应用平方差公式进行计算的是（ ）
| A、（-2m+n）（-2m-n） | ||||
B、(
| ||||
| C、（x+2y-1）（x-2y+1） | ||||
| D、（a-b）（-a+b） |
分析：可以用平方差公式计算的式子的特点是：两个二项式相乘，并且这两个二项式中有一项完全相同，另一项互为相反数．相乘的结果应该是：右边是乘式中两项的平方差（相同项的平方减去相反项的平方）．
解答：解：A、（-2m+n）（-2m-n）=-[（n+2m）（n-2m）]=-[n2-（2m）2]，符合平方差公式；
B、（
x-0.1y）（-0.1y-
x）=-（
x-0.1y）（
x+0.1y）=-[（
x）2-（0.1y）2]，符合平方差公式；
C、（x+2y-1）（x-2y+1）=[x+（2y-1）][x-（2y-1）]=x2-（2y-1）2，符合平方差公式；
D、（a-b）（-a+b）=-（b-a）（b-a）=-（b-a）2，不符合平方差公式．
故选D．
B、（
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
C、（x+2y-1）（x-2y+1）=[x+（2y-1）][x-（2y-1）]=x2-（2y-1）2，符合平方差公式；
D、（a-b）（-a+b）=-（b-a）（b-a）=-（b-a）2，不符合平方差公式．
故选D．
点评：本题考查了平方差公式，关键是要熟练掌握并灵活运用平方差公式（a+b）（a-b）=a2-b2．
练习册系列答案
53天天练系列答案
相关题目
