Question

【题目】如图，AB是⊙O的直径，C是⊙O上的一点，直线MN经过点C，过点A作直线MN的垂线，垂足为点D，且∠BAC=∠CAD．

（1）求证：直线MN是⊙O的切线；
（2）若CD=3，∠CAD=30°，求⊙O的半径．

Answer 1

【答案】
（1）

证明：连接OC，

因为OA=OC，

所以∠BAC=∠ACO．

因为AC平分∠BAD，

所以∠BAC=∠CAD，

故∠ACO=∠CAD．

所以OC∥AD，

又已知AD丄MN，

所以OC丄MN，

所以，直线MN是⊙O的切线

（2）

解：已知AB是⊙O的直径，则∠ACB=90°，

又AD丄MN，

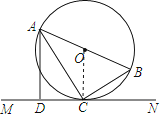
则∠ADC=90°．

因为CD=3，∠CAD=30°，

所以AD=3 ，AB=6

在Rt△ABC和Rt△ACD中，∠BAC=∠CAD，

所以Rt△ABC∽Rt△ACD，

则 ，

则AB=4 ，

所以⊙O的半径为2

【解析】（1）连接OC，推出AD∥OC，推出OC⊥MN，根据切线的判定推出即可；（2）求出AD、AC长，证△ADC∽△ACB，得出比例式，代入求出AB长即可．本题考查了切线的判定，等腰三角形的判定和性质，平行线性质，相似三角形的性质和判定的应用，主要考查学生运用定理进行推理和计算的能力．
【考点精析】解答此题的关键在于理解平行线的性质的相关知识，掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补，以及对切线的判定定理的理解，了解切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线．