题目内容
(本题11分)如图,平面直角坐标系中画出了函数l1: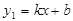 的图象。
的图象。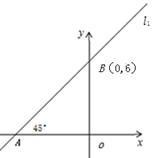
(1)根据图象,求k,b的值;
(2)请在图中画出函数l2: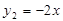 的图象;
的图象;
(3)分别过A、B两点作直线l2的垂线,垂足为E、F.
|
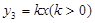 ,分别过A、B两点作直线l3的垂线,垂足为E、F.直接写出线段AE、BF、EF三者之间的关系 .
,分别过A、B两点作直线l3的垂线,垂足为E、F.直接写出线段AE、BF、EF三者之间的关系 .(5)若无论x取何值,y总取y1、y2、y3中的最大值,求y的最小值.
(1)k=1,b=6(2)见解析(3)见解析(4)AE=BF+EF(5)4
解析试题分析:
(1)k=1,b=6………2分
(2)图略(注意与坐标轴的交点位置)………4分
(3)两直线交点坐标(-2,4),………5分
与x轴交点坐标(-6,0)(0,0) S=12………6分
(4)猜想:AE=BF+EF………7分
证明:∵AE⊥OC,BF⊥OC ∴∠AEO=∠BFO
∵∠AOE+∠BOF=90° ∠BOF+∠FBO=90°∴∠AOE=∠FBO
又∵AO="BO" ∴△AOE≌△OBF (AAS) ………10 分
∴AE=OF OE="BF" ∴AE=BF+EF ………11分
(5)由题意和图形分析,此时无论取何值均是最大值,则有
X+6=-2x
X=-2,y=4
考点:图形分析
点评:此类试题最好是能画图分析,可以显而易见的看出图形中的基本交接状况,进而求解。

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 .设四边形ABPQ关于直线x=t的对称的图形与△QPC重叠
.设四边形ABPQ关于直线x=t的对称的图形与△QPC重叠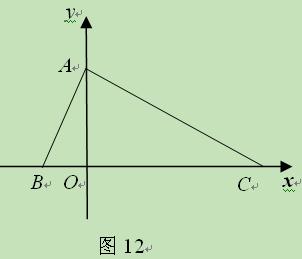
 中,
中,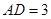 厘米,
厘米,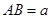 厘米(
厘米(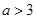 ).动点
).动点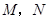 同时从
同时从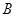 点出发,分别沿
点出发,分别沿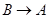 ,
, 运动,速度是
运动,速度是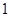 厘米/秒.过
厘米/秒.过 作直线垂直于
作直线垂直于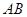 ,分别交
,分别交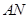 ,
, 于
于 .当点
.当点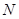 到达终点
到达终点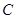 时,点
时,点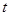 秒.
秒.
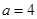 厘米,
厘米,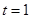 秒,求PM的长度;
秒,求PM的长度;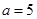 厘米,求出某个时间
厘米,求出某个时间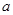 的取值范围;
的取值范围;
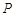 为二次函数图象上的一个动点,过点P作
为二次函数图象上的一个动点,过点P作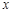 轴的垂线,垂足为D(m,0),并与直线OA交于点C.
轴的垂线,垂足为D(m,0),并与直线OA交于点C.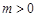 时,探索是否存在点
时,探索是否存在点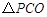 为等腰三角形,如果存在,求出
为等腰三角形,如果存在,求出