题目内容
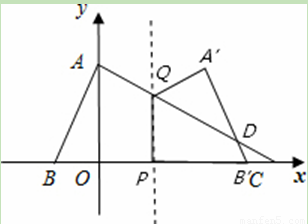
(11·大连)(本题11分)如图,在平面直角坐标系中,点A、B、C的坐标分别
为(0,2)、(-1,0)、(4,0).P是线段OC上的一动点(点P与点O、C不重合),过点P
的直线x=t与AC相交于点Q.设四边形ABPQ关于直线x=t的对称的图形与△QPC重叠
部分的面积为S.
(1)点B关于直线x=t的对称点B′的坐标为________;
(2)求S与t的函数关系式.

解:(1)(2t+1,0)…………………………2分
(2)① 如图,点B’在点C的左侧时,2t+1<4 解得t<1.5
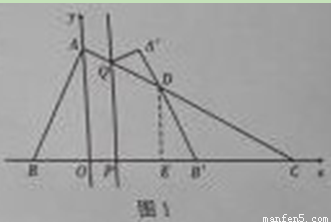
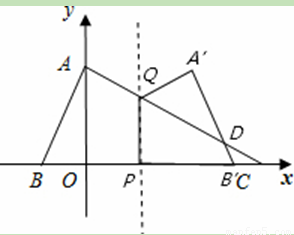
当0<t<1.5时,设点A关于直线x=t的对称点A’,A’B’与AC相交于点D,
过点D作DE⊥x轴,垂足为E,PC=4-t,B’C=4-(2t+1)=3-2t……………………3分
设直线AC解析式为y=kx+b,
将A(0,2),C(4,0)分别代入解析式得,

 由对称性可知,∠ABO=∠DB’E,又∵∠AOB=∠DEB’
由对称性可知,∠ABO=∠DB’E,又∵∠AOB=∠DEB’
∴△ABO∽△DB’E
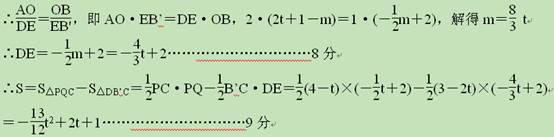 ②当1.5≤t<4时,点B’在点C的右侧或与点C重合(如图2)
②当1.5≤t<4时,点B’在点C的右侧或与点C重合(如图2)
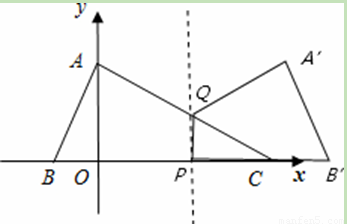
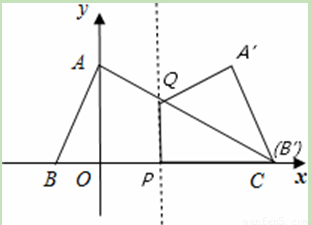
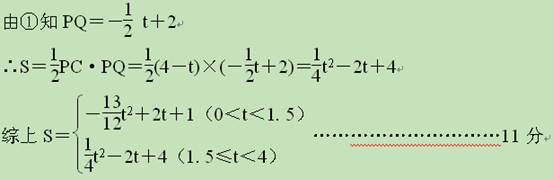 另外的解法:如图,当1.5≤t<4时,重合部分为三角形△CPQ,如图2
另外的解法:如图,当1.5≤t<4时,重合部分为三角形△CPQ,如图2
∵△CPQ∽△COA,
∵ 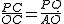 ,
,
即 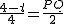 ,
,
则PQ= 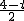 .
.
于是S△QPC= 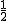 (4-t)
(4-t) 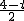 =
= 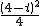 (1.5<t≤4),
(1.5<t≤4),
如图 当0<t<1.5时,重合部分为四边形DQPB’,
∵A点坐标为(0,2),
∴A′点坐标为(2t,2),
又∵B′点坐标为(2t+1,0),
设直线A′B′解析式为y=kx+b,则将A′(2t,2),
和B′(2t+1,0)分别代入解析式得, 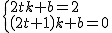 ,
,
解得k=-2,b=2+4t.
解析式为y=-2x+(2+4t),
将y=- 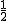 x+2和y=-x+(2+4t)组成方程组得
x+2和y=-x+(2+4t)组成方程组得 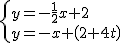 ,
,
解得 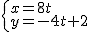 ,
,
D点坐标为(8t,-4t+2).
由于B′坐标为(2t+1,0),C点坐标为(4,0),
故B′C=4-(2t+1)=3-2t,
S△QPC= 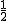 (4-t)
(4-t) 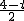 =
= 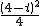 ,
,
S四边形QPB′D=S△QPC-S△DB′C= 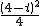 -
- 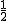 (3-2t)(-4t+2)=-
(3-2t)(-4t+2)=- 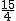 t2+6t+1(0<t≤1.5).
t2+6t+1(0<t≤1.5).
【解析】略

 阅读快车系列答案
阅读快车系列答案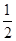 ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.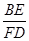 的值(用含k的式子表示).
的值(用含k的式子表示).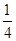 (容器各面的厚
(容器各面的厚