Question

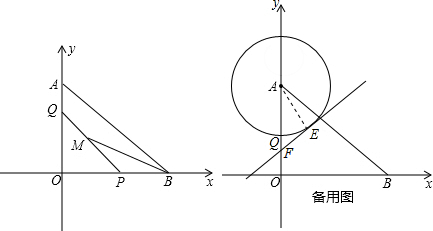
如图，在直角坐标系中，A点坐标为（0，6），B点坐标为（8，0），点P沿射线BO以每秒2个单位的速度匀速运动，同时点Q从A到O以每秒1个单位的速度匀速运动，当点Q运动到点O时两点同时停止运动．

（1）设P点运动时间为t秒，M为PQ的中点，请用t表示出M点的坐标为______；
（2）设△BPM的面积为S，当t为何值时，S有最大值，最大值为多少？
（3）请画出M点的运动路径，并说明理由；
（4）若以A为圆心，AQ为半径画圆，t为何值时⊙A与点M的运动路径只有一个交点？

Answer 1

（1）∵OP=8-2t，OQ=6-t
又∵M为PQ的中点，
∴M点的坐标为（4-t，3-

1

2

t）；

（2）BP=2t，M的纵坐标是：3-

1

2

t，
则S=

1

2

•2t•（3-

1

2

t），
即S=-

1

2

t²+3t=-

1

2

（t-3）²+

9

2

，
则当t=3时，S有最大值是

9

2

；

（3）∵M点的坐标为（4-t，3-

1

2

t），
∴M在y=

1

2

x+1上，即运动的路径是y=

1

2

x+1（-2≤x≤4）；

（4）①⊙A与点M的运动路径只有一个交点，则⊙A与射线y=

1

2

x+1相切，
∴A到直线的距离为AE=t，
设切点为E，射线y=

1

2

x+1与y轴交于点F，
则sin∠AFE=

t

5

=

2

5

，
解得：t=2

5

；
②当AQ=5时，⊙A过线段CD的端点C，
当AQ=6时，⊙A与线段CD恰有一个交点，
∴当5＜AQ≤6，即5s＜t≤6s时，⊙A与线段CD恰有一个交点，
综上所述：当t=2

5

s或5s＜t≤6s时，⊙A与线段CD恰有一个交点．