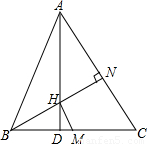
题目内容
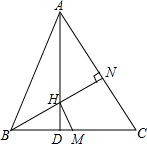 在△ABC中,H为垂心,M为BC上的中点,AD为BC上的高,且AD=BC(AC>AB).求证:HD+HM=MC.
在△ABC中,H为垂心,M为BC上的中点,AD为BC上的高,且AD=BC(AC>AB).求证:HD+HM=MC.
分析:根据题意作辅助线,根据垂心的定义及已知条件得出△ABD∽△CHD,设AD=BC=1,BD=x,则CD=1-x,根据三角形相似对应边成比例的性质得出DH,根据勾股定理分别得出HD+HM及MC,从而得出结论.
解答: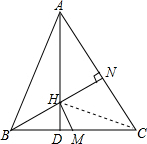 解:连CH,
解:连CH,
∵H为垂心,
∴CH⊥AB
又∵AD⊥BC,
∴△ABD∽△CHD,
设AD=BC=1,BD=x,则CD=1-x,DM=
-x,
∵
=
,
=
,
∴DH=(1-x)x,
HM2=DH2+DM2=[(1-x)x]2+(
-x)2
=[x(1-x)-
]2
∵AC>AB,BD=x<
∴x(1-x)=x-x2=-(x-
)2+
<
,
∴HM=-x(1-x)+
HD+HM=(1-x)x-x(1-x)+
=
=
=CM,
∴HD+HM=CM.
 解:连CH,
解:连CH,∵H为垂心,
∴CH⊥AB
又∵AD⊥BC,
∴△ABD∽△CHD,
设AD=BC=1,BD=x,则CD=1-x,DM=
| 1 |
| 2 |
∵
| AD |
| BD |
| CD |
| DH |
| AD |
| x |
| BC-x |
| DH |
∴DH=(1-x)x,
HM2=DH2+DM2=[(1-x)x]2+(
| 1 |
| 2 |
=[x(1-x)-
| 1 |
| 2 |
∵AC>AB,BD=x<
| 1 |
| 2 |
∴x(1-x)=x-x2=-(x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴HM=-x(1-x)+
| 1 |
| 2 |
HD+HM=(1-x)x-x(1-x)+
| 1 |
| 2 |
| 1 |
| 2 |
| BC |
| 2 |
∴HD+HM=CM.
点评:本题主要考查了垂心的性质,相似三角形的判断及对应边成比例的性质、勾股定理的应用,比较综合,难度较大.

练习册系列答案
相关题目
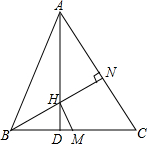 在△ABC中,H为垂心,M为BC上的中点,AD为BC上的高,且AD=BC(AC>AB).求证:HD+HM=MC.
在△ABC中,H为垂心,M为BC上的中点,AD为BC上的高,且AD=BC(AC>AB).求证:HD+HM=MC.