题目内容
在△ABC中,O为三角形内一点,D、E、F分别在BC、AC、AB上,AD、BE、CF过点O,AO:OD=2:1,则AD一定经过△ABC的( )
| A、垂心 | B、外心 | C、重心 | D、内心 |
分析:由题意,在△ABC中,O为三角形内一点,根据题意画出图形,利用相似三角形的性质及对应边长成比例和AO:OD=2:1,再根据四心的定义进行判断.
解答: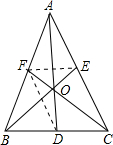 解:连接AO并延长,交BC于D,连接FE;
解:连接AO并延长,交BC于D,连接FE;
∵CF是AB边上的中线,
∴点O是三角形ABC的重心,
∴AD是BC边上的中线,
∴AF=FB,CD=DB,
∴FD是三角形ABC的中位线,
∴FD∥AC,FD=
AC,即
=
,
∴△ODF∽△OAC,
∴
=
=
,
即OC=2OF.
故选C.
 解:连接AO并延长,交BC于D,连接FE;
解:连接AO并延长,交BC于D,连接FE;∵CF是AB边上的中线,
∴点O是三角形ABC的重心,
∴AD是BC边上的中线,
∴AF=FB,CD=DB,
∴FD是三角形ABC的中位线,
∴FD∥AC,FD=
| 1 |
| 2 |
| FD |
| AC |
| 1 |
| 2 |
∴△ODF∽△OAC,
∴
| FD |
| AC |
| OF |
| OC |
| 1 |
| 2 |
即OC=2OF.
故选C.
点评:此题考查相似三角形的基本性质及对应边长成比例还涉及到三角形“四心”的定义.

练习册系列答案
相关题目
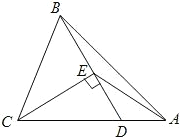
 6、如图所示,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,AQ=PQ,PR=PS.下面三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.正确的是( )
6、如图所示,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,AQ=PQ,PR=PS.下面三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.正确的是( )
 BDO.
BDO.