题目内容
 已知直线与y轴交于点B(0,1),与抛物线交于x轴上一点A,且tan∠BAO=
已知直线与y轴交于点B(0,1),与抛物线交于x轴上一点A,且tan∠BAO=| 1 | 2 |
(1)求直线和抛物线的解析式;
(2)设抛物线与x轴的另一交点为C,求△PAC的面积.
分析:(1)设直线的解析式为:y=mx+n,把A和B的坐标分别代入求出m和n的值即可,设抛物线的解析式为:y=a(x-h)2+k,由题意可知h=-3,k=-3,再把A的坐标代入即可求出a的值,进而求出抛物线的解析式;
(2)由(1)中的抛物线解析式可设y=0,即可求出点C的坐标,进而求出AC的长,又因为三角形PAB中,AC边上的高是点P的纵坐标的绝对值,利用三角形的面积公式即可求出△PAC的面积.
(2)由(1)中的抛物线解析式可设y=0,即可求出点C的坐标,进而求出AC的长,又因为三角形PAB中,AC边上的高是点P的纵坐标的绝对值,利用三角形的面积公式即可求出△PAC的面积.
解答: 解:(1)设直线的解析式为:y=mx+n,
解:(1)设直线的解析式为:y=mx+n,
∵线与y轴交于点B(0,1),与抛物线交于x轴上一点A,且tan∠BAO=
,
∴OA=2,
∴A(-2,0),
把A和B的坐标分别代入y=mx+n得:
,
解得:
,
∴直线的解析式为y=
x+1,
设抛物线的解析式为:y=a(x-h)2+k,
∵抛物线的顶点为P(-3,-3),
∴y=a(x+3)2-3,
把A(-2,0)代入得:0=a(-2+3)2-3,
∴a=3,
∴y=3(x+3)2-3;
(2)设y=0,则0=3(x+3)2-3,
∴x=-2或-4,
∴点C(-4,0),
∴OC=4
∴AC=OC-OA=2,
∴△PAC的面积为:
×AC×3=
×2×3=3.
 解:(1)设直线的解析式为:y=mx+n,
解:(1)设直线的解析式为:y=mx+n,∵线与y轴交于点B(0,1),与抛物线交于x轴上一点A,且tan∠BAO=
| 1 |
| 2 |
∴OA=2,
∴A(-2,0),
把A和B的坐标分别代入y=mx+n得:
|
解得:
|
∴直线的解析式为y=
| 1 |
| 2 |
设抛物线的解析式为:y=a(x-h)2+k,
∵抛物线的顶点为P(-3,-3),
∴y=a(x+3)2-3,
把A(-2,0)代入得:0=a(-2+3)2-3,
∴a=3,
∴y=3(x+3)2-3;
(2)设y=0,则0=3(x+3)2-3,
∴x=-2或-4,
∴点C(-4,0),
∴OC=4
∴AC=OC-OA=2,
∴△PAC的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了用待定系数法求一次函数和用顶点式求二次函数的解析式以及一次函数和二次函数的交点问题和二次函数于坐标轴的交点问题以及三角形的面积公式,题目的综合性不小,难度不大.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
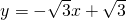 与x轴交于点A,与y轴交于点B,C是x轴上一点,如果∠ABC=∠ACB,
与x轴交于点A,与y轴交于点B,C是x轴上一点,如果∠ABC=∠ACB, 与y轴交于点A,抛物线
与y轴交于点A,抛物线 经过点A,其顶点为B,另一抛物线
经过点A,其顶点为B,另一抛物线 的顶点为D,两抛物线相交于点C
的顶点为D,两抛物线相交于点C
 的理由;
的理由;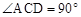 ,求m的值
,求m的值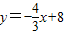 与x轴交于点A,与y轴交于点B,C是线段AB的中点.抛物线y=ax2+bx+c(a>0)过O、A两点,且其顶点的纵坐标为
与x轴交于点A,与y轴交于点B,C是线段AB的中点.抛物线y=ax2+bx+c(a>0)过O、A两点,且其顶点的纵坐标为 .
.