题目内容
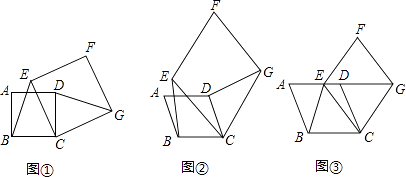
【题目】【感知】如图①,四边形ABCD、CEFG均为正方形,可知BE=DG.
【拓展】如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F,求证:BE=DG.
【应用】如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上,若AE=2ED,∠A=∠F,△EBC的面积为6,则菱形CEFG的面积为 . 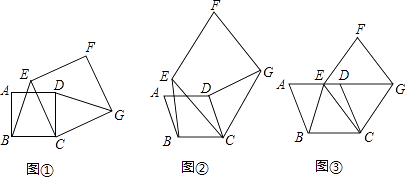
【答案】16
【解析】解:拓展:∵四边形ABCD、四边形CEFG均为菱形,
∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F.
∵∠A=∠F,
∴∠BCD=∠ECG.
∴∠BCD﹣∠ECD=∠ECG﹣∠ECD,
即∠BCE=∠DCG.
在△BCE和△DCG中,
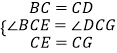 ,
,
∴△BCE≌△DCG(SAS),
∴BE=DG.
应用:∵四边形ABCD为菱形,
∴AD∥BC,
∵△BCE≌△DCG,
∴S△ABE+S△CDE=S△BEC=S△CDG=6,
∵AE=2ED,
∴S△CDE= ![]() ×6=2,
×6=2,
∴S△ECG=S△CDE+S△CDG=8,
∴S菱形CEFG=2S△ECG=16.
故答案为16.
拓展:由四边形ABCD、四边形CEFG均为菱形,利用SAS易证得△BCE≌△DCG,则可得BE=DG;
应用:由AD∥BC,△BCE≌△DCG,可得S△ABE+S△CDE=S△BEC=S△CDG=6,又由AE=2ED,可求得△CDE的面积,继而求得答案.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案【题目】某超市购进一批文具袋,每个进价为8元.试销售期间,记录的每天的销售数量与销售单价的数据如下表:
销售单价x(元) | 11 | 12 | 13 | 14 | … |
销售数量y(个) | 34 | 32 | 30 | 28 | … |
备注:物价局规定,每个文具袋的售价不低于8元且不高于18元 | |||||
(1)请你根据表中信息判断y是x的什么函数?求出其函数关系式,并写出自变量取值范围.
(2)有一天文具袋的销售单价为17元,不计其他因素,求该天销售文具袋的利润为多少元?
