题目内容
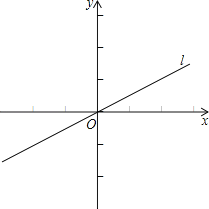
【题目】如图,在平面直角坐标系中,直线l经过原点O,且与x轴正半轴的夹角为30°,点M在x轴上,⊙M半径为2,⊙M与直线l相交于A,B两点,若△ABM为等腰直角三角形,则点M的坐标为 .
【答案】(2![]() ,0)或(﹣2
,0)或(﹣2![]() ,0).
,0).
【解析】
试题分析:先根据题意画出图形,当点M在原点右边时,过点M作MN⊥AB,得出AN2+MN2=AM2,再根据△ABM为等腰直角三角形,得出AN=MN,根据AM=2,求出MN=![]() ,最后根据直线l与x轴正半轴的夹角为30°,求出OM=2
,最后根据直线l与x轴正半轴的夹角为30°,求出OM=2![]() ,即可得出点M的坐标,当点M在原点左边时,根据点M′与点M关于原点对称,即可得出点M′的坐标.
,即可得出点M的坐标,当点M在原点左边时,根据点M′与点M关于原点对称,即可得出点M′的坐标.
解:如图;当点M在原点右边时,
过点M作MN⊥AB,垂足为N,
则AN2+MN2=AM2,
∵△ABM为等腰直角三角形,
∴AN=MN,
∴2MN2=AM2,
∵AM=2,
∴2MN2=22,
∴MN=![]() ,
,
∵直线l与x轴正半轴的夹角为30°,
∴OM=2![]() ,
,
∴点M的坐标为(2![]() ,0),
,0),
当点M在原点左边时,
则点M′与点M关于原点对称,
此时点M′的坐标为(﹣2![]() ,0),
,0),
故答案为;(2![]() ,0)或(﹣2
,0)或(﹣2![]() ,0).
,0).


练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目