Question

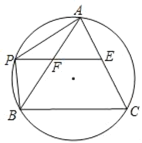
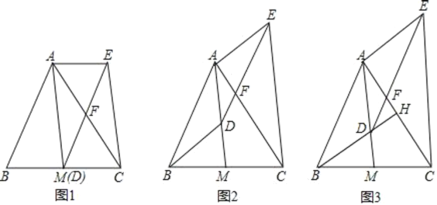
【题目】如图，AM是△ABC的中线，D是线段AM上一点（不与点A重合）．DE∥AB交AC于点F，CE∥AM，连接AE．

（1）如图1，当点D与M重合时，求证：四边形ABDE是平行四边形；

（2）如图2，当点D不与M重合时，（1）中的结论还成立吗？请说明理由．

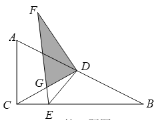
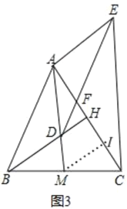
（3）如图3，延长BD交AC于点H，若BH⊥AC，且BH＝AM，求∠CAM的度数．

Answer 1

【答案】（1）见解析；（2）结论成立，理由见解析；（3）∠CAM＝30°．

【解析】

（1）根据DE∥AB，CE∥AM，同位角相等，又BD＝DC，可证得△ABD≌△EDC，继而证得结论；

（2）作MG∥DE交CE于G，易证四边形DMGE是平行四边形，利用(1)的方法证得△ABD≌△EDC，继而证得结论；

（3）取线段CH的中点I，连接MI，证得MI＝BH＝AM，MI⊥AC，易证得结论.

（1）∵DE∥AB，

∴∠EDC＝∠ABM，

∵CE∥AM，

∴∠ECD＝∠ADB，

∵AM是△ABC的中线，且D与M重合，

∴BD＝DC，

∴△ABD≌△EDC，

∴AB＝ED，

∵AB∥ED，

∴四边形ABDE是平行四边形；

（2）结论成立，理由如下：

如图2，

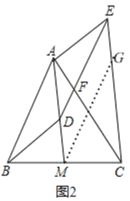
过点M作MG∥DE交CE于G，

∵CE∥AM，

∴四边形DMGE是平行四边形，

∴ED＝GM，且ED∥GM，

∵MG∥DE∥AB

∴∠GMC＝∠ABM，

∵CG∥AM，

∴∠GCM＝∠AMB，

∵AM是△ABC的中线，

∴BM＝MC，

∴△ABM≌△GMC，

∴AB＝GM，AB∥GM，

∴AB∥DE，AB＝DE，

∴四边形ABDE是平行四边形；

（3）如图3取线段CH的中点I，连接MI，

∵BM＝MC，

∴MI是△BHC的中位线，

∴MI∥BH，MI＝BH，

∵BH⊥AC，且BH＝AM，

∴MI＝AM，MI⊥AC，

∴∠CAM＝30°．