题目内容
已知a<0,二次函数y=-ax2的图象上有三个点A(-2,y1),B(1,y2),C(3,y3),则有
- A.y1<y2<y3
- B.y2<y3<y1
- C.y3<y2<y1
- D.y2<y1<y3
D
分析:由二次函数y=-ax2可知,此函数的对称轴为x=0,顶点坐标为(0,0),二次项系数-a>0,故此函数的图象开口向上,有最小值;函数图象上的点与y轴越接近,则函数值越小,因而比较A、B、C三点与对称轴的距离的大小即可.
解答:函数的对称轴为x=0,二次函数y=-ax2开口向上,有最小值,
∵A到对称轴x=0的距离是2;
B到对称轴x=0的距离是1;
C到对称轴x=0的距离是3.
∴y3>y1>y2.
故选D.
点评:本题考查了二次函数图象上点的坐标特征,属于基础题,关键是(1)找到二次函数的对称轴;(2)掌握二次函数y=ax2+bx+c(a≠0)的图象性质.
分析:由二次函数y=-ax2可知,此函数的对称轴为x=0,顶点坐标为(0,0),二次项系数-a>0,故此函数的图象开口向上,有最小值;函数图象上的点与y轴越接近,则函数值越小,因而比较A、B、C三点与对称轴的距离的大小即可.
解答:函数的对称轴为x=0,二次函数y=-ax2开口向上,有最小值,
∵A到对称轴x=0的距离是2;
B到对称轴x=0的距离是1;
C到对称轴x=0的距离是3.
∴y3>y1>y2.
故选D.
点评:本题考查了二次函数图象上点的坐标特征,属于基础题,关键是(1)找到二次函数的对称轴;(2)掌握二次函数y=ax2+bx+c(a≠0)的图象性质.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
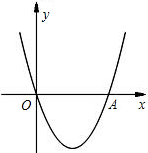 已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.
已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.
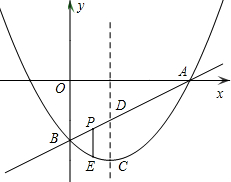 段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.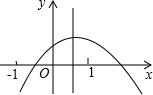 已知,如图:二次函数的图象如图所示,给出以下结论:
已知,如图:二次函数的图象如图所示,给出以下结论: