题目内容
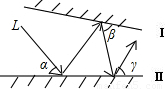
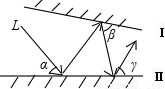
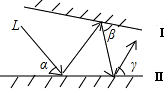 如图所示,光线L照射到平面镜I上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=55°,∠γ=75°,则∠β为
如图所示,光线L照射到平面镜I上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=55°,∠γ=75°,则∠β为
- A.50°
- B.55°
- C.60°
- D.65°
D
分析:根据入射光线与水平线的夹角等于反射光线与水平线的夹角,三角形的内角和是180°求解.
解答:∠β所在的顶点处是一个平角为180°,α,γ经过反射后,与β所在的顶点处的一个角组成三角形的内角和180°,
即180°-2β+α+γ=180°,
∴2β=∠α+∠γ
∴∠β=(55+75)÷2=65°.
故选D.
点评:入射光线与水平线的夹角等于反射光线与水平线的夹角,注意隐含的180°的关系的使用.
分析:根据入射光线与水平线的夹角等于反射光线与水平线的夹角,三角形的内角和是180°求解.
解答:∠β所在的顶点处是一个平角为180°,α,γ经过反射后,与β所在的顶点处的一个角组成三角形的内角和180°,
即180°-2β+α+γ=180°,
∴2β=∠α+∠γ
∴∠β=(55+75)÷2=65°.
故选D.
点评:入射光线与水平线的夹角等于反射光线与水平线的夹角,注意隐含的180°的关系的使用.

练习册系列答案
相关题目
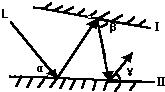 11、如图所示,光线L照射到平面镜I上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=55°,∠γ=75°,则∠β为( )
11、如图所示,光线L照射到平面镜I上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=55°,∠γ=75°,则∠β为( )