题目内容
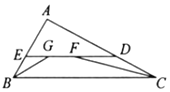
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一点,
内一点,![]() ,
,![]() 为
为![]() 延长线上的一点,且
延长线上的一点,且![]() .
.
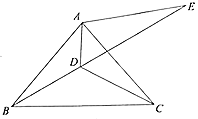
(1)求![]() 的度数;
的度数;
(2)求证:![]() 平分
平分![]() ;
;
(3)请判断![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)![]() ;(2)见解析;(3)结论:
;(2)见解析;(3)结论:![]() ,见解析.
,见解析.
【解析】
(1)由等腰三角形的性质可得∠ABC=∠ACB,根据角的和差关系可得∠DBC=∠DCB,可得BD=CD,利用SAS可证明△ADB≌△ADC,可得∠BAD=∠CAD,即可求出∠BAD的度数;
(2)利用三角形外角性质可得∠ADE=60°,根据三角形内角和定理可得∠ABC=∠ACB=50°,即可得出![]() =30°,利用外角性质可得∠CDE=60°,即可证明∠ADE=∠CDE,可得
=30°,利用外角性质可得∠CDE=60°,即可证明∠ADE=∠CDE,可得![]() 平分
平分![]() ;
;
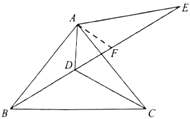
(3)在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,根据等腰三角形的性质可得∠ABE=∠E,由DF=DA,∠ADE=60°可证明△ADF是等边三角形,可得
,根据等腰三角形的性质可得∠ABE=∠E,由DF=DA,∠ADE=60°可证明△ADF是等边三角形,可得![]() ,利用AAS可证明
,利用AAS可证明![]() ,可得BD=EF,即可证明
,可得BD=EF,即可证明![]() .
.
(1)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中, ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() .
.
(3)结论:![]() ,
,
在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目