题目内容
若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形底角的度数为分析:因为三角形的高有三种情况,而直角三角形不合题意,故舍去,所以应该分两种情况进行分析,从而得到答案.
解答:解:(1)当等腰三角形是锐角三角形时,腰上的高在三角形内部,如图,
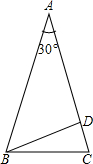
BD为等腰三角形ABC腰AC上的高,并且BD=
AB,
根据直角三角形中30°角的对边等于斜边的一半的逆用,可知顶角为30°,此时底角为75°;
(2)当等腰三角形是钝角三角形时,腰上的高在三角形外部,如图,
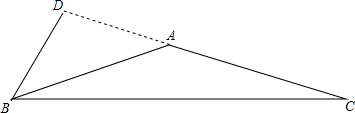
BD为等腰三角形ABC腰AC上的高,并且BD=
AB,
根据直角三角形中30°角的对边等于斜边的一半的逆用,可知顶角的邻补角为30°,此时顶角是150°,底角为15°.
故其底角为15°或75°.

BD为等腰三角形ABC腰AC上的高,并且BD=
| 1 |
| 2 |
根据直角三角形中30°角的对边等于斜边的一半的逆用,可知顶角为30°,此时底角为75°;
(2)当等腰三角形是钝角三角形时,腰上的高在三角形外部,如图,

BD为等腰三角形ABC腰AC上的高,并且BD=
| 1 |
| 2 |
根据直角三角形中30°角的对边等于斜边的一半的逆用,可知顶角的邻补角为30°,此时顶角是150°,底角为15°.
故其底角为15°或75°.
点评:此题主要考查等腰三角形的性质;正确的分类讨论是解答本题的关键.

练习册系列答案
相关题目
若等腰三角形一腰上的高等于腰长的一半,则这个三角形的底角为( )
| A、30° | B、75° | C、30°或60° | D、75°或15° |