题目内容
下表是小亮所填实验报告的部分内容:
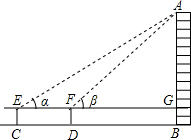
已知测倾器的高CE=DF=1m,请根据小亮测得的数据填表,并根据平均值计算国贸大厦的高AB.(结果保留根号)
| 课题 | 在平面上测量国贸大厦的高AB | |||
| 测 量 示 意 图 |
 | |||
| 测 得 数 据 |
测量项目 | ∠α | ∠β | CD的长 |
| 第一次 | 30°16′ | 44°35′ | 60.11m | |
| 第二次 | 29°44′ | 45°25′ | 59.89m | |
| 平均值 | ||||
分析:首先求出各角度以及线段的平均值,进而利用锐角三角函数关系求出AG的长,进而得出答案.
解答: 解:∠α=(30°16′+29°44′)÷2=30°,∠β=(44°35′+45°25′)÷2=45°,
解:∠α=(30°16′+29°44′)÷2=30°,∠β=(44°35′+45°25′)÷2=45°,
CD=(60.11+59.89)÷2=60(m),
∴EC=FD=BG=1m,
设AG=x,则FG=x,EF=CD=60m,
故tanα=
=
=
,
解得:x=30
+30
∴AB=AG+BG=30
+30+1=31+30
,
答:国贸大厦的高AB为31+30
m.
 解:∠α=(30°16′+29°44′)÷2=30°,∠β=(44°35′+45°25′)÷2=45°,
解:∠α=(30°16′+29°44′)÷2=30°,∠β=(44°35′+45°25′)÷2=45°,CD=(60.11+59.89)÷2=60(m),
∴EC=FD=BG=1m,
设AG=x,则FG=x,EF=CD=60m,
故tanα=
| AG |
| EG |
| x |
| 60+x |
| ||
| 3 |
解得:x=30
| 3 |
∴AB=AG+BG=30
| 3 |
| 3 |
答:国贸大厦的高AB为31+30
| 3 |
点评:此题主要考查了解直角三角形的应用,根据已知选择正确的三角函数关系是解题关键.

练习册系列答案
相关题目
下表是小亮所填实习报告的部分内容:
请根据小亮测得的数据,填表并计算国贸大厦的高(已知测倾器的高CE=DF=1m).
| 题目 | 在平面上测量国贸大厦的高AB | |||
| 测量目标 | 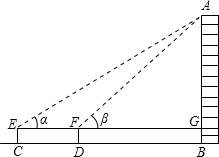 | |||
| 测量数据 | 测量项目 | ∠α | ∠β | CD的长 |
| 第一次 | 30°16′ | 44°35′ | 60.11m | |
| 第二次 | 29°44′ | 45°25′ | 59.89m | |
| 平均值 | 30° | 45° | 60m | |
下表是小亮所填实验报告的部分内容:
| 课题 | 在平面上测量国贸大厦的高AB | |||
| 测 量 示 意 图 |  | |||
| 测 得 数 据 | 测量项目 | ∠α | ∠β | CD的长 |
| 第一次 | 30°16′ | 44°35′ | 60.11m | |
| 第二次 | 29°44′ | 45°25′ | 59.89m | |
| 平均值 | ||||
(2004•太原)下表是小亮所填实习报告的部分内容:
请根据小亮测得的数据,填表并计算国贸大厦的高(已知测倾器的高CE=DF=1m).
| 题目 | 在平面上测量国贸大厦的高AB | |||
| 测量目标 |  | |||
| 测量数据 | 测量项目 | ∠α | ∠β | CD的长 |
| 第一次 | 30°16′ | 44°35′ | 60.11m | |
| 第二次 | 29°44′ | 45°25′ | 59.89m | |
| 平均值 | 30° | 45° | 60m | |