题目内容
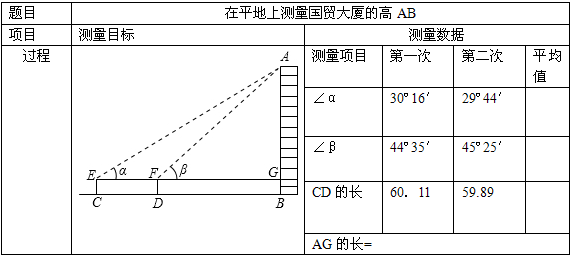
下表是小亮所填实习报告的部分内容:| 题目 | 在平面上测量国贸大厦的高AB | |||
| 测量目标 | 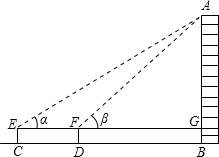 | |||
| 测量数据 | 测量项目 | ∠α | ∠β | CD的长 |
| 第一次 | 30°16′ | 44°35′ | 60.11m | |
| 第二次 | 29°44′ | 45°25′ | 59.89m | |
| 平均值 | 30° | 45° | 60m | |
分析:根据图表就可以计算出∠α、∠β、CD的均值,即它们的值.FG、GE根据三角函数都可以利用三角函数用AG表示出来.已知CD,就得到一个关于AG的方程,解方程就可以求出AG,则可以得到AB.
解答:解:根据条件可知∠α=30°,∠β=45° CD=60m.
在直角△AFG中,BD=FG=
=AG,
在直角△AEG中,EG=
AG
∵CD=EG-FG
∴
AG-AG=60
解得AG=30
+30m.
∴AB=30
+30+1=30
+31(m).
在直角△AFG中,BD=FG=
| AG |
| tanβ |
在直角△AEG中,EG=
| 3 |
∵CD=EG-FG
∴
| 3 |
解得AG=30
| 3 |
∴AB=30
| 3 |
| 3 |
点评:解直角梯形可以通过作高线转化为解直角三角形和矩形的问题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
下表是小亮所填实习报告的部分内容:
| 题目 | 在平面上测量国贸大厦的高AB | |||
| 测量目标 | 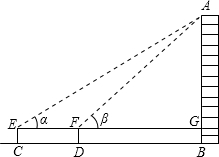 | |||
| 测量数据 | 测量项目 | ∠α | ∠β | CD的长 |
| 第一次 | 30°16′ | 44°35′ | 60.11m | |
| 第二次 | 29°44′ | 45°25′ | 59.89m | |
| 平均值 | 30° | 45° | 60m | |
(2004•太原)下表是小亮所填实习报告的部分内容:
请根据小亮测得的数据,填表并计算国贸大厦的高(已知测倾器的高CE=DF=1m).
| 题目 | 在平面上测量国贸大厦的高AB | |||
| 测量目标 |  | |||
| 测量数据 | 测量项目 | ∠α | ∠β | CD的长 |
| 第一次 | 30°16′ | 44°35′ | 60.11m | |
| 第二次 | 29°44′ | 45°25′ | 59.89m | |
| 平均值 | 30° | 45° | 60m | |
(2004•太原)下表是小亮所填实习报告的部分内容:
请根据小亮测得的数据,填表并计算国贸大厦的高(已知测倾器的高CE=DF=1m).
| 题目 | 在平面上测量国贸大厦的高AB | |||
| 测量目标 | 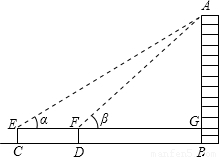 | |||
| 测量数据 | 测量项目 | ∠α | ∠β | CD的长 |
| 第一次 | 30°16′ | 44°35′ | 60.11m | |
| 第二次 | 29°44′ | 45°25′ | 59.89m | |
| 平均值 | 30° | 45° | 60m | |