Question

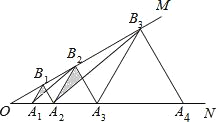
【题目】如图，已知∠MON=30°，点A1、A2、A3在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，分别连接A1B2，连接A2B3…．若OA1=a，从左往右的阴影面积依次记作S1、S2、S3…Sn．则Sn= ．

Answer 1

【答案】a2．

【解析】

试题解析：∵△A1B1A2是等边三角形，∴∠B1A1A2=60°．

∵∠MON=30°，∴∠OB1A1=60°-30°=30°，

∴∠A1OB1=∠A1B1O，∴B1A=OA1=a．

同理：A2B2=OA2=2a，B3A3=OA3=4a，…

BnAn=2n-1a，

∴S正△AnBnAn+1=BnAn2=（2n-1a）2．

=22n-2a2=4n-1a2=4n-2a2．

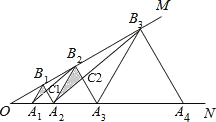
∵△A1B1A2、△A2B2A3为等边三角形，

∴∠B1A1A2=∠B2A2A3=60°，

∴A1B1∥A2B2，

∴△A1B1C1∽△B2A2C1，

∴，

∴，

∴，即S1=S△A1B1A2．

同理可得Sn=S△AnBnAn+1=4n-2a2=a2．