题目内容
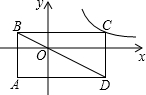 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=| k |
| x |
| A、-2 | B、4 | C、3 | D、2 |
分析:可以设点C的坐标是(m,n),根据题干条件可知△BMO∽△BAD,于是得到mn=4,又知点(m,n)在反比例函数y=
的图象上,即可求出k的值.
| k |
| x |
解答: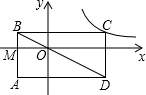 解:可以设点C的坐标是(m,n),
解:可以设点C的坐标是(m,n),
设AB与x轴交于点M,则△BMO∽△BAD,
则
=
,
因为AD=2+m,AB=2+n,OM=2,BM=n,
因而得到
=
,
即mn=4,
点(m,n)在反比例函数y=
的图象上,
代入得到:k=xy=mn=4,
故选B.
 解:可以设点C的坐标是(m,n),
解:可以设点C的坐标是(m,n),设AB与x轴交于点M,则△BMO∽△BAD,
则
| BM |
| AB |
| OM |
| AD |
因为AD=2+m,AB=2+n,OM=2,BM=n,
因而得到
| n |
| 2+n |
| 2 |
| 2+m |
即mn=4,
点(m,n)在反比例函数y=
| k |
| x |
代入得到:k=xy=mn=4,
故选B.
点评:本题主要考查了反比例函数的知识点,反比例函数系数k的几何意义为:反比例函数图象上的点的横纵坐标之积是定值k,同时|k|也是该点到两坐标轴的垂线段与两坐标轴围成的矩形面积,本题综合性强,考查知识面广,能较全面考查学生综合应用知识的能力.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
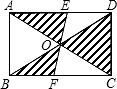 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为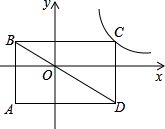 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y= 如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线
如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线 (2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( )
(2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( ) 如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=
如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=