题目内容
【题目】将纸片△ABC沿DE折叠使点A落在A′处的位置.
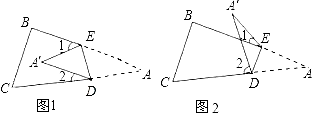
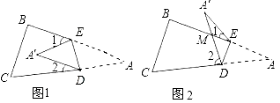
(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是 .
(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.
【答案】(1)2∠A=∠1+∠2,(2)2∠A=∠2;(3)2∠A=∠2-∠1.
【解析】
试题分析:(1)根据折叠性质得出∠AED=∠A′ED,∠ADE=∠A′DE,根据三角形内角和定理得出∠AED+∠ADE=180°-∠A,代入∠1+∠2=180°+180°-2(∠AED+∠ADE)求出即可;
(2)根据三角形外角性质得出∠DME=∠A′+∠1,∠2=∠A+∠DME,代入即可求出答案.
试题解析:(1)图1中,2∠A=∠1+∠2,
理由是:∵延DE折叠A和A′重合,
∴∠AED=∠A′ED,∠ADE=∠A′DE,
∵∠AED+∠ADE=180°-∠A,∠1+∠2=180°+180°-2(∠AED+∠ADE),
∴∠1+∠2=360°-2=2∠A;
(2)2∠A=∠2,如图2
∠2=∠A+∠EA′D=2∠A,
(3)如图3,2∠A=∠2-∠1,
理由是:∵延DE折叠A和A′重合,
∴∠A=∠A′,
∵∠DME=∠A′+∠1,∠2=∠A+∠DME,
∴∠2=∠A+∠A′+∠1,
即2∠A=∠2-∠1.


练习册系列答案
相关题目