题目内容
若菱形ABCD的对角线AC长为10cm,且菱形ABCD的周长为52cm,则另一条对角线BD长为
24
24
cm,其面积S=120
120
cm2.分析:菱形对角线互相垂直平分,故△ABE为直角三角形,根据菱形周长可以计算AB的值,在Rt△ABE中,已知AB,AE根据勾股定理可以计算BE的长,根据BE即可计算BD的长,根据菱形的对角线的长度即可计算菱形ABCD的面积.
解答: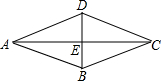 解:(1)菱形对角线互相垂直平分,
解:(1)菱形对角线互相垂直平分,
故△ABE为直角三角形,
菱形ABCD的周长为52cm,
则AB=13cm,
∵AC=10cm,
∴AE=5cm,
在Rt△ABE中,AB=13cm,AE=5cm,
∴BE=
=12cm,
∴BD=2BE=24cm;
(2)菱形的对角线长为BD=10cm,AC=24cm,
∴菱形ABCD的面积S=
BD•AC=
×10cm×24cm=120cm2,
故答案为:24cm,120cm2.
 解:(1)菱形对角线互相垂直平分,
解:(1)菱形对角线互相垂直平分,故△ABE为直角三角形,
菱形ABCD的周长为52cm,
则AB=13cm,
∵AC=10cm,
∴AE=5cm,
在Rt△ABE中,AB=13cm,AE=5cm,
∴BE=
| AB2-BE2 |
∴BD=2BE=24cm;
(2)菱形的对角线长为BD=10cm,AC=24cm,
∴菱形ABCD的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:24cm,120cm2.
点评:本题考查了勾股定理在直角三角形中的运用,考查了菱形对角线互相平分的性质,本题中正确计算BE的长是解题的关键.

练习册系列答案
相关题目


 ,求BC的长.
,求BC的长.


 ,求BC的长.
,求BC的长.


 ,求BC的长.
,求BC的长.


 ,求BC的长.
,求BC的长.