题目内容
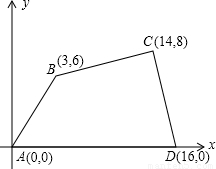
如图14所示,在直角坐标系中,O是坐标原点,点A在y轴正半轴上,二次函数y=ax2+[x/6]+c的图象F交x轴于B、C两点,交y轴于M点,其中B(-3,0),M(0,-1)。已知AM=BC。
[1]求二次函数的解析式;
[2]证明:在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形,并请求出直线BD的解析式;
[3]在[2]的条件下,设直线l过D且分别交直线BA、BC于不同的P、Q两点,AC、BD相交于N。
①若直线l⊥BD,如图14所示,试求[1/BP]+[1/BQ]的值;
②若l为满足条件的任意直线。如图15所示,①中的结论还成立吗?若成立,证明你的猜想;若不成立,请举出反例。
 |
解:[1]∵二次函数y=ax2+1 6 x+c的图象经过点B[-3,0],M[0,-1],
∴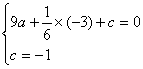 ,
,
解得a=1/6 ,c=-1。
∴二次函数的解析式为:y= [![]() x2/6]+[x/6]-1。
x2/6]+[x/6]-1。
[2]由二次函数的解析式为:y=[x2/6]+[x/6]-1,
令y=0,得[x2/6]+[x/6]-1=0,
解得x1=-3,x2=2,∴C[2,0),∴BC=5;
令x=0,得y=-1,∴M[0,-1],OM=1。
又AM=BC,∴OA=AM-OM=4,∴A[0,4]。
设AD∥x轴,交抛物线于点D,如图1所示,
则yD=[x2/6]+[x/![]() 6]-1=OA=4,
6]-1=OA=4,
解得x1=5,x2=-6[位于第二象限,舍去]
∴D点坐标为[5,4]。
∴AD=BC=5,
又∵AD∥BC,
∴四边形ABCD为平行四边形。
即在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形。
设直线BD解析式为:y=kx+b,∵B[-3,0],D[5,4],
∴![]() ,
,
解得:k=1/2 ,b=3/2,
∴直线BD解析式为:y=[x/2]+[3/2]。
[3]在Rt△AOB中,AB=![]() =5,又AD=BC=5,∴▱ABCD是菱形。
=5,又AD=BC=5,∴▱ABCD是菱形。
①若直线l⊥BD,如图14所示.
∵四边形ABCD是菱形,
∴AC⊥BD,
∴AC∥直线l,
∴BA/BP=BC/BQ=BN/BD=1/2,
∵BA=BC=5,
∴BP=BQ=10,
∴1/BP+1/BQ=[1/10]+[1/10]=1/5;
②若l为满足条件的任意直线,如图15所示,此时①中的结论依然成立,理由如下:
∵AD∥BC,CD∥AB,
∴△PAD∽△DCQ,
∴AP/CD=AD/CQ,
∴AP•CQ=AD•CD=5×5=25。
∴[1/BP]+[1/BQ]=(1/[AB+AP])+(1/[BC+CQ])
=(1/[5+AP])+(1/[5+CQ])
=([5+AP]+[5+CQ])/([5+AP][5+CQ])
=10+AP+CQ 25+5(AP+CQ)+AP•CQ
=[10+AP+CQ]/(50+5[AP+CQ])
=1/5。

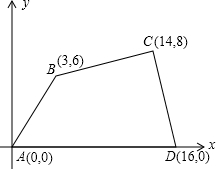 如图所示,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),确定这个四边形的面积.
如图所示,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),确定这个四边形的面积.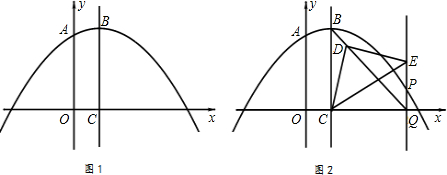
 如图所示,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),确定这个四边形的面积.
如图所示,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),确定这个四边形的面积.