题目内容
若直线y=kx+3与坐标轴所围成的三角形的面积为12,则k的值为________.
±
分析:由直线的性质可知,当x=0时,可知函数与y轴的交点为(0,3),设图象与x轴的交点到原点的距离为a,根据三角形的面积为12,求出a的值,从而求出k的值.
解答:当x=0时,可知函数与y轴的交点为(0,3),
设图象与x轴的交点到原点的距离为a,
则 ×3a=12,
×3a=12,
a=8.
则函数与x轴的交点为(8,0)或(-8,0).
把(8,0)代入y=kx+3得,8k+3=0,k=- ;
;
把(-8,0)代入y=kx+3得,-8k+3=0,k= .
.
故答案为± .
.
点评:此题考查了一次函数图象上点的坐标特征,及直线与坐标轴的交点问题,解答时要注意进行分类讨论.

分析:由直线的性质可知,当x=0时,可知函数与y轴的交点为(0,3),设图象与x轴的交点到原点的距离为a,根据三角形的面积为12,求出a的值,从而求出k的值.
解答:当x=0时,可知函数与y轴的交点为(0,3),
设图象与x轴的交点到原点的距离为a,
则
 ×3a=12,
×3a=12,a=8.
则函数与x轴的交点为(8,0)或(-8,0).
把(8,0)代入y=kx+3得,8k+3=0,k=-
 ;
;把(-8,0)代入y=kx+3得,-8k+3=0,k=
 .
.故答案为±
 .
.点评:此题考查了一次函数图象上点的坐标特征,及直线与坐标轴的交点问题,解答时要注意进行分类讨论.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
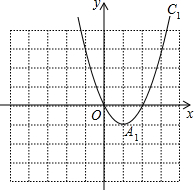 已知抛物线C1:y=x2-2x的图象如图所示,把C1的图象沿y轴翻折,得到抛物线C2的图象,抛物线C1与抛物线C2的图象合称图象C3.
已知抛物线C1:y=x2-2x的图象如图所示,把C1的图象沿y轴翻折,得到抛物线C2的图象,抛物线C1与抛物线C2的图象合称图象C3.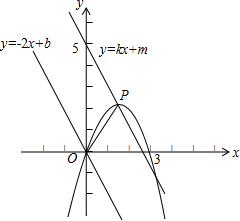 (2013•贵阳模拟)如图,一次函数y=-2x+b的图象与二次函数y=-x2+3x+c的图象都经过原点,
(2013•贵阳模拟)如图,一次函数y=-2x+b的图象与二次函数y=-x2+3x+c的图象都经过原点,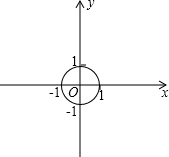 如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,在此直角坐标系中画直线y=kx+2,若直线y=kx+2与⊙O相切,则k=
如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,在此直角坐标系中画直线y=kx+2,若直线y=kx+2与⊙O相切,则k=