题目内容
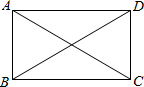 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?分析:根据矩形性质求出AC=BD=13cm,根据已知得出OA+OB+AB+OB+OC+BC+OC+OD+DC+OD+OA+AD=86cm,推出AB+BC+CD+DA=86-2(AC+BD),代入求出即可.
解答:解:∵四边形ABCD是矩形,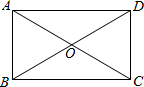
∴AC=BD=13cm,
∵△AOB、△BOC、△COD和△AOD四个三角形的周长和为86cm,
∴OA+OB+AB+OB+OC+BC+OC+OD+DC+OD+OA+AD=86cm,
∴AB+BC+CD+DA=86-2(AC+BD)
=86-4×13
=34(cm).
答:矩形ABCD的周长等于34cm.

∴AC=BD=13cm,
∵△AOB、△BOC、△COD和△AOD四个三角形的周长和为86cm,
∴OA+OB+AB+OB+OC+BC+OC+OD+DC+OD+OA+AD=86cm,
∴AB+BC+CD+DA=86-2(AC+BD)
=86-4×13
=34(cm).
答:矩形ABCD的周长等于34cm.
点评:本题考查了矩形的性质的应用,关键是得出AB+BC+CD+DA=86-2(AC+BD),注意:矩形的对角线相等.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 9、如图,矩形ABCD被分割成六个正方形,其中最小正方形的面积等于1,则矩形ABCD的面积等于( )
9、如图,矩形ABCD被分割成六个正方形,其中最小正方形的面积等于1,则矩形ABCD的面积等于( )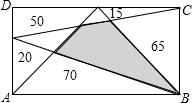 如图,矩形ABCD被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为
如图,矩形ABCD被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为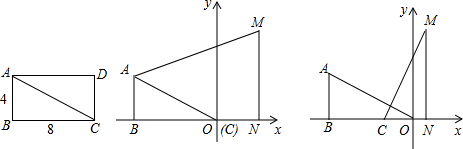
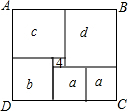 如图,矩形ABCD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,其他正方形的边长分别为a、b、c、d.求矩形ABCD中最大正方形与最小正方形的面积之差.
如图,矩形ABCD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,其他正方形的边长分别为a、b、c、d.求矩形ABCD中最大正方形与最小正方形的面积之差.