题目内容
在一个不透明的盒子中,共有“一白三黑”四枚围棋子,它们除颜色外无其他区别.
(1)随机地从盒子中取出1枚,则取出的是白子的概率是多少?
(2)随机地从盒子中取出1枚,不放回再取出第二枚,请用画树状图或列表的方式表示出所有等可能的结果,并求出恰好取到“两枚棋子颜色不相同”的概率是多少?
(1)随机地从盒子中取出1枚,则取出的是白子的概率是多少?
(2)随机地从盒子中取出1枚,不放回再取出第二枚,请用画树状图或列表的方式表示出所有等可能的结果,并求出恰好取到“两枚棋子颜色不相同”的概率是多少?
(1) ;(2)
;(2)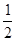
 ;(2)
;(2)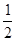
试题分析:(1)根据盒子中共有“一白三黑”四枚围棋子结合概率公式即可求得结果;
(2)先根据画树状图或列表的方式表示出所有等可能的结果,再根据概率公式即可求得结果.
(1)由题意得
 (取出的是白子)=
(取出的是白子)= ;
;(2)解法一:画树状图:

P( 一黑一白)=
 .
.解法二:列表:
| | 白 | 黑1 | 黑2 | 黑3 | ||
| 白 | | (白,黑1) | (白,黑2) | (白,黑3) | ||
| 黑1 | (黑1,白) | | (黑1,黑2) | (黑1,黑3) | ||
| 黑2 | (黑2,白) | (黑2,黑1) | | (黑2,黑3) | ||
| 黑3 | (黑3,白) | (黑3,黑1) | (黑3,黑2) | | ||
 .
.点评:解题的关键是熟练掌握概率的求法:概率=所求情况数与总情况数的比.

练习册系列答案
相关题目
 ,求n的值.
,求n的值.
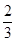 ,则n的值是________.
,则n的值是________.