题目内容
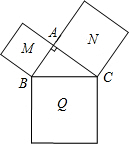 如图,由Rt△ABC的三边向外作正方形,若最大正方形Q的边长为13,正方形N的边长为12,则正方形M的面积为( )
如图,由Rt△ABC的三边向外作正方形,若最大正方形Q的边长为13,正方形N的边长为12,则正方形M的面积为( )分析:由正方形的面积公式可知SN=AC2,SQ=BC2,SM=AB2,在Rt△ABC中,由勾股定理得AC2+AB2=BC2,即SN+SM=SQ,由此可求SM.
解答:解:∵在Rt△ABC中,AC2+AB2=BC2,
又由正方形面积公式得SN=AC2=144,SQ=BC2=169,SM=AB2,
∴SM=SQ-SN=169-144=25.
故选C.
又由正方形面积公式得SN=AC2=144,SQ=BC2=169,SM=AB2,
∴SM=SQ-SN=169-144=25.
故选C.
点评:本题考查了勾股定理及正方形面积公式的运用,解题关键是明确直角三角形的边长的平方即为相应的正方形的面积,难度一般.

练习册系列答案
相关题目
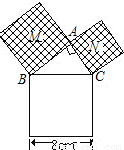
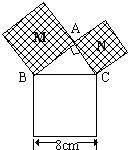 8、如图,由Rt△ABC的三边向外作正方形,若最大正方形的边长为8cm,则正方形M与正方形N的面积之和为
8、如图,由Rt△ABC的三边向外作正方形,若最大正方形的边长为8cm,则正方形M与正方形N的面积之和为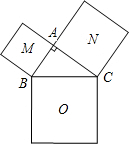 如图,由Rt△ABC的三边向外作正方形,若最大正方形O的边长为13,正方形N的边长为12,则正方形M的面积为
如图,由Rt△ABC的三边向外作正方形,若最大正方形O的边长为13,正方形N的边长为12,则正方形M的面积为